Đại Số: Nền Tảng Toán Học và Ứng Dụng Bất Ngờ Trong Cuộc Sống | scantruyen.com

Đại Số: Nền Tảng Toán Học và Những Ứng Dụng Đa Dạng

Đại số là một nhánh quan trọng của toán học, nghiên cứu các hệ thống trừu tượng được gọi là cấu trúc đại số và sự biến đổi của các biểu thức trong những hệ thống này. Nó không chỉ là sự mở rộng của số học mà còn là nền tảng cho nhiều lĩnh vực khoa học và kỹ thuật khác.

Đại Số Sơ Cấp: Bước Đầu Làm Quen

Đại số sơ cấp, thường được giảng dạy tại trường phổ thông, tập trung vào việc giải các phương trình chứa biến số. Mục tiêu chính là tìm ra các giá trị của biến số để phương trình trở thành một mệnh đề đúng. Quá trình này sử dụng nhiều phương pháp biến đổi phương trình để cô lập biến, giúp học sinh làm quen với tư duy logic và giải quyết vấn đề.

Đại Số Tuyến Tính: Giải Quyết Hệ Phương Trình

Đại số tuyến tính là một lĩnh vực chuyên sâu hơn, tập trung vào việc nghiên cứu các phương trình tuyến tính và hệ phương trình tuyến tính. Nó cung cấp các công cụ mạnh mẽ để tìm ra nghiệm của hệ phương trình, đồng thời phân tích các tập hợp nghiệm này. Đại số tuyến tính có ứng dụng rộng rãi trong nhiều lĩnh vực như khoa học máy tính, kỹ thuật và kinh tế.

Đại Số Trừu Tượng: Khám Phá Cấu Trúc Toán Học

Đại số trừu tượng đi sâu vào việc nghiên cứu các cấu trúc đại số, bao gồm các tập hợp toán học và các phép toán được định nghĩa trên chúng. Đây là một dạng khái quát hóa của đại số sơ cấp và đại số tuyến tính, mở rộng phạm vi nghiên cứu sang các đối tượng toán học không phải số và các phép toán phi số học. Các cấu trúc đại số như nhóm, vành và trường được phân biệt dựa trên số lượng phép toán và các quy tắc mà chúng tuân theo.

Lịch Sử Phát Triển của Đại Số

Phương pháp đại số đã được nghiên cứu từ thời cổ đại để giải quyết các bài toán thực tế trong nhiều lĩnh vực, đặc biệt là hình học. Các nhà toán học thời kỳ sau đó đã tập trung vào việc tìm kiếm các kỹ thuật giải phương trình tổng quát, không gắn liền với ứng dụng cụ thể nào. Việc phát triển một hệ thống ký hiệu biểu tượng nghiêm ngặt vào thế kỷ 16 và 17 đã đánh dấu một bước tiến quan trọng trong lịch sử đại số. Đến giữa thế kỷ 19, phạm vi của đại số đã mở rộng đáng kể, bao gồm nhiều loại phép toán và cấu trúc đại số khác nhau.

Liên Hệ Giữa Đại Số và Các Lĩnh Vực Khác

Đại số có mối liên hệ mật thiết với nhiều lĩnh vực khác của toán học, bao gồm hình học, tô pô, lý thuyết số và vi tích phân. Ngoài ra, nó còn có ứng dụng trong các lĩnh vực tra vấn khác như logic và khoa học thực nghiệm, chứng tỏ tầm quan trọng và tính ứng dụng cao của đại số trong đời sống và công nghệ.

Toán Math

Đại Số: Nguồn Gốc, Định Nghĩa và Sự Phát Triển

Đại số, một nhánh quan trọng của toán học, không chỉ là việc giải phương trình mà còn là nền tảng cho nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này sẽ đi sâu vào định nghĩa, nguồn gốc và sự phát triển của đại số, đồng thời làm rõ sự khác biệt giữa các cấp độ trừu tượng của nó.

Định Nghĩa và Cấu Trúc Đại Số

Đại số nghiên cứu các cấu trúc đại số và các phép toán được thực hiện trên chúng. Một cấu trúc đại số bao gồm một tập hợp các đối tượng toán học (ví dụ: số nguyên) cùng với các phép toán đại số (như cộng và nhân) được định nghĩa trên tập hợp đó. Đại số khám phá các quy luật, đặc điểm chung và các loại cấu trúc đại số khác nhau. Nó cũng tập trung vào việc nghiên cứu các biến số trong phương trình và cách thức biến đổi các phương trình này.

Từ Nguyên và Lịch Sử Hình Thành

Thuật ngữ "đại số" có nguồn gốc từ cuốn sách Al-Jabr của nhà toán học người Ba Tư Muhammad ibn Mūsā al-Khwārizmī vào thế kỷ 9. Ban đầu, "al-jabr" có nghĩa là "phục hồi" hoặc "hoàn thiện", ám chỉ việc hoàn thành một phương trình bằng cách chuyển các số hạng. Cuốn sách này mô tả một phương pháp giải phương trình và trở thành nền tảng cho sự phát triển của đại số sau này. Từ "algebra" du nhập vào tiếng Anh từ tiếng Ả Rập qua tiếng Latinh và các ngôn ngữ châu Âu khác vào thế kỷ 16.

Các Cấp Độ Trừu Tượng của Đại Số

Đại số có nhiều cấp độ trừu tượng khác nhau:

• Đại số sơ cấp: Là dạng suy rộng của số học, tập trung vào các phép toán trên số thực và sử dụng biến số để biểu diễn các đại lượng không xác định.
• Đại số trừu tượng: Nghiên cứu các cấu trúc đại số như nhóm, vành và trường, không bị giới hạn ở một miền số cụ thể.
• Đại số phổ dụng: Có độ trừu tượng cao hơn, nghiên cứu các đặc trưng chung của các cấu trúc đại số mà không quan tâm đến các cấu trúc cụ thể.

Đại Số Trong Ngôn Ngữ Việt Nam

Trong tiếng Việt, "đại số" là từ Hán-Việt (代數; dàishù) có nghĩa là "môn toán học dùng chữ thay số để suy tìm cái quan hệ của số".

Đại số không chỉ là một công cụ toán học mà còn là chìa khóa mở ra cánh cửa cho nhiều lĩnh vực khác, từ khoa học máy tính đến kinh tế học. Việc hiểu rõ các khái niệm và nguyên tắc của đại số là vô cùng quan trọng đối với bất kỳ ai muốn theo đuổi sự nghiệp trong các lĩnh vực này.

Đại Số Sơ Cấp: Nền Tảng Toán Học và Ứng Dụng Thực Tế

Giới thiệu về Đại Số Sơ Cấp

Đại số sơ cấp là hình thức đại số lâu đời nhất và cơ bản nhất, đóng vai trò nền tảng cho các lĩnh vực toán học cao hơn. Nó mở rộng số học bằng cách sử dụng các biến số (hay còn gọi là "biến" hoặc "ẩn") để biểu diễn các đại lượng chưa biết hoặc chưa được xác định. Nhờ đó, chúng ta có thể diễn đạt các quan hệ toán học tổng quát và giải quyết các bài toán phức tạp một cách hiệu quả.

Số Học và Sự Xuất Hiện của Biến Số

Số học tập trung vào các phép toán trên các con số, như cộng, trừ, nhân, chia, lũy thừa, khai căn và logarit. Ví dụ, 2 + 5 = 7 là một phép toán số học cơ bản. Tuy nhiên, đại số sơ cấp đi xa hơn bằng cách giới thiệu biến số. Biến số là ký hiệu đại diện cho một giá trị chưa biết. Ví dụ, phương trình 2 × 3 = 3 × 2 thuộc về số học, nhưng khi thay các số bằng biến, ta có thể diễn đạt tính chất giao hoán của phép nhân: a × b = b × a. Đây là một luật tổng quát áp dụng cho mọi số.

Các Thành Phần Của Biểu Thức Đại Số

Biểu thức đại số được tạo thành từ các số, biến và các phép toán. Các thành phần chính bao gồm:

• Hằng số: Một giá trị cố định, ví dụ: c.
• Biến số: Ký hiệu đại diện cho một đại lượng chưa biết, ví dụ: x, y.
• Hệ số: Số nhân với biến, ví dụ: 5 trong biểu thức 5x.
• Hạng tử: Một phần của biểu thức được phân tách bởi các phép cộng hoặc trừ, ví dụ: 5x và 3 trong biểu thức 5x + 3.
• Toán tử: Ký hiệu thực hiện một phép toán, ví dụ: +, -, ×, ÷.
• Hạng tử không đổi: Một hằng số không nhân với biến, ví dụ: 3 trong biểu thức 5x + 3.

Ví dụ về biểu thức đại số: 5x + 3, 32xyz, 64x₁² + 7x₂ - c.

Phương Trình và Bất Đẳng Thức

Phương trình là một mệnh đề so sánh hai biểu thức bằng nhau, sử dụng dấu bằng (=). Ví dụ: 5x² + 6x = 3y + 4. Bất đẳng thức so sánh hai biểu thức bằng các ký hiệu khác nhau, như < (nhỏ hơn), > (lớn hơn), hoặc ≠ (khác). Ví dụ: x² = 4 đúng khi x = 2 hoặc x = -2, và sai trong các trường hợp khác. Phương trình có thể là đồng nhất (luôn đúng) hoặc có điều kiện (chỉ đúng với một số giá trị nhất định).

Giải Phương Trình: Tìm Giá Trị Ẩn

Mục tiêu chính của đại số sơ cấp là tìm giá trị của biến số để một phương trình hoặc bất đẳng thức trở thành đúng. Điều này được thực hiện bằng cách biến đổi phương trình theo các quy tắc nhất định, ví dụ như cộng hoặc trừ cùng một giá trị cho cả hai vế. Một nguyên tắc quan trọng là thực hiện cùng một phép toán trên cả hai vế để duy trì sự cân bằng. Ví dụ, để giải phương trình x - 7 = 4, ta cộng cả hai vế cho 7 để được x = 11.

Các Kỹ Thuật Giải Phương Trình

Có nhiều kỹ thuật để giải phương trình, bao gồm:

• Đơn giản hóa: Thay thế một biểu thức phức tạp bằng một biểu thức tương đương đơn giản hơn.
• Phép thế: Thay một biến bằng một biểu thức tương đương.

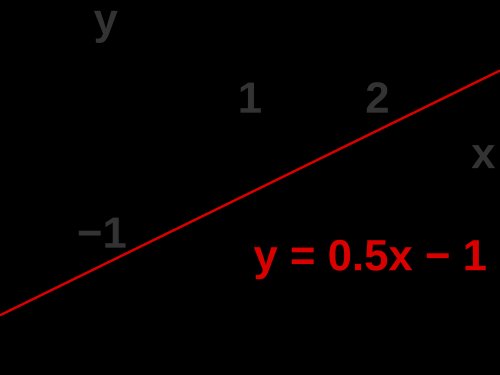
Ứng Dụng Hình Học của Đại Số

Phương trình đại số có thể được biểu diễn bằng hình học thông qua đồ thị. Mỗi cặp giá trị (x, y) thỏa mãn phương trình được biểu diễn bằng một điểm trên đồ thị. Ví dụ, phương trình y = 0.5x - 1 có thể được vẽ thành một đường thẳng trên hệ tọa độ, với mỗi điểm trên đường thẳng đại diện cho một nghiệm của phương trình.

Đa thức: Khái niệm cơ bản và ứng dụng trong giải phương trình

Đa thức là một biểu thức toán học quan trọng, được xây dựng từ các hạng tử bao gồm hằng số, biến số và tích của chúng. Một ví dụ điển hình của đa thức là

x⁴ + 3xy² + 5x³ - 1. Đa thức có thể có một hoặc nhiều biến, và mỗi biến có thể được nâng lên lũy thừa nguyên dương.

Các loại đa thức

Đa thức được phân loại dựa trên số lượng hạng tử:

• Đơn thức: Đa thức chỉ có một hạng tử.
• Nhị thức: Đa thức có hai hạng tử.
• Tam thức: Đa thức có ba hạng tử.

Bậc của đa thức được xác định bởi lũy thừa lớn nhất của biến trong các hạng tử của nó. Ví dụ, đa thức x⁴ + 3xy² + 5x³ - 1 có bậc là 4. Đa thức bậc một còn được gọi là đa thức tuyến tính, đóng vai trò quan trọng trong đại số tuyến tính.

Phân tích nhân tử và ứng dụng

Phân tích nhân tử là quá trình viết lại đa thức dưới dạng tích của các nhân tử. Việc này giúp đơn giản hóa đa thức và dễ dàng tìm ra các giá trị của biến làm cho đa thức bằng 0. Ví dụ, đa thức x² - 3x - 10 có thể được phân tích thành (x + 2)(x - 5). Do đó, đa thức này bằng 0 khi x = -2 hoặc x = 5.

Giải phương trình đa thức

Trước thế kỷ 19, việc giải phương trình đa thức (phương trình mà đa thức bằng 0) là một lĩnh vực trọng tâm của đại số. Các nhà toán học đã tìm cách biểu diễn nghiệm của phương trình thông qua căn bậc n. Công thức nghiệm bậc hai ax² + bx + c = 0 là một ví dụ điển hình:

x = (-b ± √(b² - 4ac)) / 2a

Các công thức nghiệm cho bậc ba và bậc bốn cũng đã được tìm ra. Tuy nhiên, theo định lý Abel–Ruffini được chứng minh vào thế kỷ 19, không tồn tại công thức nghiệm tổng quát cho phương trình đa thức bậc cao hơn bốn. Trong trường hợp này, các phương pháp số học như phương pháp Newton–Raphson được sử dụng để tìm nghiệm gần đúng.

Định lý cơ bản của đại số

Định lý cơ bản của đại số khẳng định rằng mọi phương trình đa thức một ẩn bậc dương với hệ số thực hoặc phức luôn có ít nhất một nghiệm phức. Điều này có nghĩa là mọi đa thức bậc dương có thể được phân tích thành tích của các đa thức tuyến tính. Định lý này được chứng minh vào đầu thế kỷ 19, mặc dù nó không cung cấp phương pháp cụ thể để tính toán nghiệm.

Đại Số Tuyến Tính: Nền Tảng Toán Học Cho Thế Giới Hiện Đại

Đại số tuyến tính, thoạt nghe có vẻ khô khan, lại là một lĩnh vực toán học vô cùng quan trọng, đóng vai trò nền tảng trong nhiều ngành khoa học kỹ thuật hiện đại. Bài viết này sẽ đi sâu vào những khái niệm cơ bản của đại số tuyến tính, từ hệ phương trình tuyến tính đến ma trận, và cách chúng được ứng dụng trong thực tế.

Hệ Phương Trình Tuyến Tính: Bước Khởi Đầu

Đại số tuyến tính bắt đầu với việc nghiên cứu các hệ phương trình tuyến tính. Một phương trình được gọi là tuyến tính khi nó có thể được biểu diễn dưới dạng:

a₁x₁ + a₂x₂ + ... + a_nx_n = b

Trong đó, a₁, a₂, ..., a_n và b là các hằng số. Ví dụ:

• x₁ - 7x₂ + 3x₃ = 0
• (1/4)x - y = 4

Hệ phương trình tuyến tính là một tập hợp các phương trình tuyến tính, và mục tiêu là tìm ra các giá trị của các biến (x₁, x₂, ..., x_n) thỏa mãn tất cả các phương trình trong hệ.

Ma Trận: Công Cụ Biểu Diễn và Giải Quyết

Để đơn giản hóa việc biểu diễn và giải quyết các hệ phương trình tuyến tính, người ta sử dụng ma trận. Ma trận là một mảng các số được sắp xếp theo hàng và cột. Ví dụ, hệ phương trình sau:

9x₁ + 3x₂ - 13x₃ = 0

2.3x₁ + 7x₃ = 9

-5x₁ - 17x₂ = -3

Có thể được viết gọn lại dưới dạng ma trận:

AX = B

Trong đó:

A =

[

9   3   -13

2.3   0   7

-5   -17   0

]

X =

[

x₁

x₂

x₃

]

B =

[

0

9

-3

]

Các phép toán trên ma trận (cộng, nhân, nghịch đảo) cho phép chúng ta giải quyết hệ phương trình tuyến tính một cách hiệu quả. Một trong những phương pháp phổ biến là tìm ma trận nghịch đảo A^-1 sao cho A^-1A = I (I là ma trận đơn vị), sau đó tính nghiệm của hệ phương trình là X = A^-1B.

Không Gian Vectơ và Ánh Xạ Tuyến Tính: Mở Rộng Khái Niệm

Nghiên cứu về không gian vectơ và ánh xạ tuyến tính là một phần quan trọng của đại số tuyến tính. Không gian vectơ là một tập hợp các đối tượng (vectơ) cùng với các phép toán cộng và nhân vô hướng thỏa mãn một số tính chất nhất định. Ánh xạ tuyến tính là một hàm giữa các không gian vectơ bảo toàn các phép toán cộng và nhân vô hướng.

Trong không gian vectơ hữu hạn chiều, vectơ và ánh xạ tuyến tính có thể được biểu diễn bằng ma trận. Điều này cho thấy mối liên hệ mật thiết giữa lý thuyết ma trận và lý thuyết không gian vectơ.

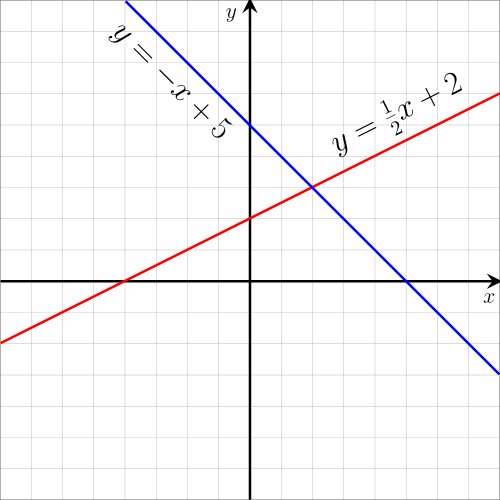
Ứng Dụng Hình Học và Thực Tế

Hệ phương trình tuyến tính hai ẩn có thể được biểu diễn bằng các đường thẳng trên mặt phẳng. Nghiệm của hệ là giao điểm của các đường thẳng này. Nếu các đường thẳng song song hoặc trùng nhau, hệ phương trình có thể vô nghiệm hoặc có vô số nghiệm.

Đại số tuyến tính có ứng dụng rộng rãi trong nhiều lĩnh vực như:

• Khoa học máy tính: Xử lý ảnh, đồ họa máy tính, học máy, trí tuệ nhân tạo.
• Kỹ thuật: Phân tích mạch điện, cơ học kết cấu, xử lý tín hiệu.
• Kinh tế: Mô hình hóa kinh tế, tối ưu hóa nguồn lực.
• Thống kê: Phân tích hồi quy, phân tích thành phần chính.

Từ việc giải quyết các bài toán đơn giản đến việc xây dựng các mô hình phức tạp, đại số tuyến tính là một công cụ mạnh mẽ và không thể thiếu trong thế giới hiện đại.

Đại Số Trừu Tượng: Khám Phá Nền Tảng Toán Học Hiện Đại

Đại số trừu tượng, hay còn được biết đến với tên gọi đại số hiện đại, là một lĩnh vực nghiên cứu sâu rộng về các cấu trúc đại số. Thay vì tập trung vào việc giải các phương trình cụ thể như đại số sơ cấp, đại số trừu tượng đi sâu vào việc nghiên cứu bản chất của các phép toán và mối quan hệ giữa chúng.

Cấu Trúc Đại Số Là Gì?

Cấu trúc đại số có thể được hiểu là một khuôn mẫu giúp chúng ta hiểu rõ hơn về cách các phép toán hoạt động trên các đối tượng toán học. Ví dụ, phép cộng các số là một phép toán, và đại số trừu tượng nghiên cứu các phép toán tổng quát hơn, không chỉ giới hạn ở số học.

Điểm khác biệt chính giữa đại số trừu tượng và các nhánh đại số khác (như đại số sơ cấp hay đại số tuyến tính) nằm ở tính tổng quát. Đại số trừu tượng không chỉ xem xét các cấu trúc cụ thể mà còn so sánh, đối chiếu và phân loại các cấu trúc đại số khác nhau, chẳng hạn như nhóm, vành và trường. Sự khác biệt giữa các cấu trúc này nằm ở số lượng phép toán mà chúng sử dụng và các quy tắc mà chúng tuân theo.

Phép Toán Hai Ngôi: Nền Tảng Của Đại Số Trừu Tượng

Nhiều cấu trúc đại số dựa trên khái niệm phép toán hai ngôi. Đây là một phép toán nhận hai đối tượng đầu vào và tạo ra một đối tượng đầu ra duy nhất. Phép cộng và phép nhân là những ví dụ quen thuộc về phép toán hai ngôi.

Ở cấp độ hình thức, một cấu trúc đại số bao gồm một tập hợp (tập nền) và một hoặc nhiều phép toán. Đại số trừu tượng đặc biệt quan tâm đến phép toán hai ngôi, vì chúng là nền tảng cho nhiều cấu trúc quan trọng. Ví dụ, cấu trúc ⟨ℕ, +⟩, trong đó ℕ là tập hợp các số tự nhiên và + là phép cộng, là một ví dụ đơn giản về cấu trúc đại số sử dụng phép toán hai ngôi.

Ứng Dụng và Mở Rộng

Tập nền trong một cấu trúc đại số không nhất thiết phải chứa các số. Nó có thể chứa bất kỳ loại đối tượng toán học nào, và các phép toán cũng không bị giới hạn ở các phép toán số học thông thường. Ví dụ, trong nhóm đối xứng của một hình học, tập nền bao gồm các phép biến đổi hình học (như phép quay), và phép toán hai ngôi là hàm hợp (áp dụng lần lượt hai phép biến đổi).

Trong giáo dục toán học, đại số trừu tượng thường là một học phần nâng cao dành cho sinh viên chuyên ngành toán sau khi họ đã hoàn thành các khóa học về đại số tuyến tính.

Lý thuyết nhóm, vành và trường: Nền tảng của Đại số trừu tượng

Đại số trừu tượng là một lĩnh vực cốt lõi của toán học, tập trung vào việc nghiên cứu các cấu trúc đại số. Các cấu trúc này được định nghĩa bởi các luật và tiên đề mà chúng tuân theo, cùng với số lượng phép toán được sử dụng. Trong số đó, lý thuyết nhóm, lý thuyết vành và lý thuyết trường là những trụ cột quan trọng, cung cấp nền tảng cho nhiều lĩnh vực toán học khác và ứng dụng thực tế.

Lý thuyết nhóm: Khám phá tính chất của phép toán

Nhóm là một trong những cấu trúc đại số cơ bản nhất. Một nhóm bao gồm một tập hợp và một phép toán thỏa mãn bốn tính chất quan trọng:

• Tính kết hợp: (a ∘ b) ∘ c = a ∘ (b ∘ c)
• Phần tử đơn vị: Tồn tại một phần tử e sao cho a ∘ e = e ∘ a = a
• Phần tử nghịch đảo: Với mỗi phần tử a, tồn tại một phần tử a^-1 sao cho a ∘ a^-1 = a^-1 ∘ a = e

Ví dụ, tập hợp số nguyên ⟨Z, +⟩ cùng với phép cộng là một nhóm. Phần tử đơn vị là 0, và phần tử nghịch đảo của một số a bất kỳ là -a. Tuy nhiên, tập hợp số tự nhiên cùng với phép cộng không tạo thành một nhóm vì không có phần tử nghịch đảo cho các số nguyên dương.

Lý thuyết nhóm nghiên cứu bản chất của nhóm, với các định lý quan trọng như định lý cơ bản của các nhóm Abel hữu hạn và định lý Feit–Thompson. Định lý Feit–Thompson, chứng minh rằng mọi nhóm hữu hạn đơn lẻ đều có cấp bậc là lũy thừa của một số nguyên tố, là một thành tựu toán học lớn trong thế kỷ 20.

Lý thuyết vành và trường: Mở rộng khái niệm phép toán

Vành là một cấu trúc đại số với hai phép toán, tương tự như phép cộng và phép nhân của số. Vành là một nhóm giao hoán dưới phép cộng, và phép nhân có tính kết hợp và phân phối theo phép cộng. Vành số nguyên (Z) là một ví dụ đơn giản về vành giao hoán.

Trường là một vành giao hoán mà trong đó mọi phần tử khác không đều có nghịch đảo phép nhân. Các tập hợp số hữu tỉ, số thực và số phức đều tạo thành trường với phép cộng và phép nhân. Vành số nguyên không phải là một trường vì không có nghịch đảo phép nhân cho mọi phần tử.

Lý thuyết vành nghiên cứu các khái niệm như vành con, vành thương, vành đa thức và i-đê-an, cùng với định lý cơ sở Hilbert. Lý thuyết trường tập trung vào các trường, mở rộng trường, đóng đại số và trường hữu hạn. Lý thuyết Galois khám phá mối quan hệ giữa lý thuyết trường và lý thuyết vành, dựa trên định lý cơ bản của lý thuyết Galois.

Những lý thuyết này không chỉ là những khái niệm toán học trừu tượng mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực như mật mã học, vật lý, khoa học máy tính và kỹ thuật.

Lý thuyết về Quan hệ Tương hỗ giữa các Cấu trúc Đại số: Một Tổng quan Dễ Hiểu

Đại số không chỉ dừng lại ở những phép tính đơn thuần với số. Nó còn là một thế giới của các cấu trúc, mỗi cấu trúc có những quy tắc và tính chất riêng. Bài viết này sẽ cung cấp một cái nhìn tổng quan về mối quan hệ giữa các cấu trúc đại số, từ những khái niệm cơ bản đến những ứng dụng nâng cao, đặc biệt hướng đến đối tượng là sinh viên mới bắt đầu làm quen với đại số trừu tượng.

Các Cấu trúc Đại số Cơ bản

Ngoài nhóm, vành và trường quen thuộc, đại số còn nghiên cứu nhiều cấu trúc khác như magma, nửa nhóm, monoid, nhóm Abel, vành giao hoán, mô đun, dàn, không gian vectơ, đại số trên một trường, đại số kết hợp và đại số phi kết hợp. Sự khác biệt giữa chúng nằm ở loại đối tượng được mô tả và các ràng buộc mà các phép toán phải thỏa mãn. Ví dụ:

• Magma: Một tập hợp với một phép toán hai ngôi.
• Nửa nhóm: Một magma có tính kết hợp.
• Monoid: Một nửa nhóm có phần tử đơn vị.
• Nhóm: Một monoid mà mọi phần tử đều có phần tử nghịch đảo.

Mối quan hệ giữa các cấu trúc này thể hiện ở việc một cấu trúc cơ bản có thể "nâng cấp" lên cấu trúc phức tạp hơn bằng cách thỏa mãn thêm các yêu cầu. Chẳng hạn, một magma trở thành nửa nhóm khi phép toán của nó có tính kết hợp.

Đồng cấu và Đẳng cấu: So sánh các Cấu trúc

Để hiểu rõ hơn về mối liên hệ giữa các cấu trúc, chúng ta sử dụng khái niệm đồng cấu. Đồng cấu là một hàm bảo toàn cấu trúc, tức là nó ánh xạ các phần tử sao cho phép toán trong cấu trúc mới tương ứng với phép toán trong cấu trúc cũ. Nếu đồng cấu là song ánh (một-một và toàn ánh), ta gọi nó là đẳng cấu. Đẳng cấu cho thấy hai cấu trúc đại số thực chất là "giống nhau" về mặt cấu trúc, chỉ khác nhau về cách ký hiệu.

Đại số Con: Thu hẹp Phạm vi

Một cách khác để so sánh các cấu trúc là thông qua khái niệm đại số con. Đại số con là một tập con của một cấu trúc đại số lớn hơn, cùng với phép toán được thừa hưởng từ cấu trúc lớn hơn. Điều quan trọng là đại số con phải "đóng" dưới phép toán, nghĩa là phép toán trên các phần tử của đại số con phải luôn cho ra kết quả thuộc đại số con đó. Ví dụ, tập hợp các số chẵn là một đại số con của tập hợp các số nguyên dưới phép cộng.

Đại số Phổ dụng và Lý thuyết Phạm trù: Cái nhìn Tổng quan

Đại số phổ dụng nghiên cứu các cấu trúc đại số một cách tổng quát, không quan tâm đến bản chất cụ thể của các phần tử mà chỉ tập trung vào các phép toán và các đồng nhất thức (phương trình luôn đúng). Lý thuyết phạm trù cung cấp một khuôn khổ còn rộng lớn hơn để mô tả mối quan hệ giữa các đối tượng toán học, không chỉ giới hạn trong đại số. Nó sử dụng khái niệm phạm trù, bao gồm các đối tượng và các "mũi tên" (cấu xạ) giữa chúng.

Lý thuyết phạm trù được ứng dụng rộng rãi trong toán học hiện đại, cung cấp một cách tiếp cận thống nhất để hiểu các khái niệm toán học cốt lõi.

Lịch sử Đại số: Từ Cuộn Giấy Rhind Đến Đại Số Trừu Tượng

Đại số, một nhánh quan trọng của toán học, không ra đời một cách đột ngột mà là kết quả của quá trình phát triển lâu dài, bắt nguồn từ nhu cầu giải quyết các bài toán thực tế trong cuộc sống hàng ngày. Lịch sử của đại số là một hành trình khám phá đầy thú vị, trải qua nhiều nền văn minh và các nhà toán học lỗi lạc.

Những Bước Đầu Tiên: Ai Cập Cổ Đại và Babylon

Một trong những tài liệu cổ xưa nhất liên quan đến đại số là Cuộn giấy Rhind của Ai Cập cổ đại, có niên đại khoảng năm 1650 TCN. Cuộn giấy này chứa các bài toán liên quan đến việc giải phương trình tuyến tính, ví dụ như bài toán tìm một đại lượng khi biết một phần tư của nó cộng với chính nó bằng 15. Cùng thời kỳ, các phiến đất sét Babylon đã thể hiện các phương pháp giải phương trình tuyến tính và đa thức bậc hai bằng phương pháp phần bù bình phương.

Sự Tiếp Nối và Phát Triển ở Hy Lạp và Trung Quốc

Nhiều kiến thức từ Babylon và Ai Cập được truyền đến Hy Lạp cổ đại. Tuy nhiên, người Hy Lạp tập trung chủ yếu vào hình học, nhưng vẫn sử dụng các phương pháp đại số để giải quyết các bài toán hình học. Diophantus, nhà toán học Hy Lạp sống vào thế kỷ 3 CN, đã có những đóng góp quan trọng trong việc giải phương trình đại số và là người đầu tiên sử dụng ký hiệu biểu tượng để biểu diễn đa thức. Đồng thời, tại Trung Quốc cổ đại, Cửu chương toán thuật, được biên soạn từ thế kỷ 10 TCN đến thế kỷ 2 CN, đã khám phá nhiều kỹ thuật giải phương trình đại số, bao gồm cả ý tưởng tương tự như xây dựng ma trận hiện đại.

Đại Số Ả Rập: Bước Ngoặt Quan Trọng

Một bước ngoặt quan trọng trong lịch sử đại số là sự xuất hiện của đại số Ả Rập. Nhà toán học Ba Tư al-Khwārizmī, với cuốn sách "Cuốn cẩm nang về tính toán bằng hoàn thiện và cân bằng" (năm 825 CN), đã trình bày các phương pháp chung để giải phương trình bậc nhất và bậc hai bằng cách "giảm trừ" và "cân bằng" hai vế. Đây được xem là nền tảng của đại số hiện đại. Các nhà toán học Ả Rập khác như Thābit ibn Qurra và Omar Khayyám cũng có những đóng góp đáng kể.

Ấn Độ và Sự Ra Đời Số 0

Tại Ấn Độ, Brahmagupta đã nghiên cứu cách giải phương trình bậc hai và hệ phương trình nhiều ẩn từ thế kỷ 7, đồng thời là người đầu tiên sử dụng số 0 và số âm trong phương trình đại số. Các phương pháp của Brahmagupta được hoàn thiện hơn bởi Mahāvīra và Bhāskara II vào các thế kỷ sau. Nhà toán học Trung Quốc Tần Cửu Thiều vào năm 1247 đã phát triển thuật toán tính giá trị của đa thức, bao gồm cả đa thức bậc cao.

Sự Phát Triển ở Châu Âu và Đại Số Trừu Tượng

Nhà toán học Ý Fibonacci đã mang các ý tưởng của al-Khwārizmī sang châu Âu. Đến thế kỷ 16, Gerolamo Cardano xuất bản Ars Magna, một tác phẩm quan trọng về đại số, bao gồm cả việc giải phương trình bậc ba và bậc bốn. Các nhà toán học Pháp François Viète và René Descartes đã phát minh hệ ký hiệu biểu tượng để biểu diễn phương trình một cách trừu tượng và súc tích hơn. Thế kỷ 19 chứng kiến sự phát triển của đại số trừu tượng, tập trung vào nghiên cứu các cấu trúc đại số tổng quát, với những đóng góp quan trọng từ các nhà toán học như David Hilbert, Emil Artin và Garrett Birkhoff.

Từ đó đến nay, đại số tiếp tục phát triển mạnh mẽ, với nhiều lĩnh vực mới như đại số phổ dụng, đại số tô pô, đại số đồng điều và lý thuyết phạm trù, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật.

Ứng Dụng Rộng Rãi của Đại Số: Từ Toán Học đến Khoa Học và Đời Sống

Đại số không chỉ là một nhánh của toán học thuần túy mà còn là công cụ mạnh mẽ với tầm ảnh hưởng sâu rộng trong nhiều lĩnh vực khác nhau. Quá trình đại số hóa toán học, tức là áp dụng các phương pháp và nguyên lý đại số vào các lĩnh vực toán học khác như hình học, tô pô, lý thuyết số và vi tích phân, đã mở ra những khả năng mới trong việc mô hình hóa và giải quyết các vấn đề phức tạp.

Đại Số trong Các Lĩnh Vực Toán Học

Việc sử dụng ký hiệu dưới dạng biến số giúp các nhà toán học biểu diễn tri thức ở mức độ tổng quát hơn, tạo điều kiện phát triển các mô hình hình thức để mô tả mối tương tác giữa các đối tượng.

Hình Học Đại Số

Hình học đại số sử dụng biểu thức đại số để mô tả các đối tượng hình học. Ví dụ, phương trình y = 3x - 7 biểu diễn một đường thẳng, còn x2 + y2 + z2 = 1 biểu diễn một mặt cầu. Đặc biệt, đa tạp đại số, tập nghiệm của hệ phương trình đa thức, được sử dụng để mô tả các đối tượng hình học phức tạp. Việc giải các bài toán hình học cũng trở nên dễ dàng hơn nhờ các lập luận đại số, chẳng hạn như xác định giao điểm giữa đường thẳng và đường tròn.

Tô Pô Đại Số

Tô pô học nghiên cứu tính chất bất biến của đối tượng hình học dưới các phép biến đổi liên tục. Tô pô đại số sử dụng các lý thuyết đại số, như lý thuyết nhóm, để phân loại không gian tô pô. Nhóm đồng luân, ví dụ, phân loại không gian dựa trên sự tồn tại của các nút hoặc lỗ.

Lý Thuyết Số Đại Số

Lý thuyết số đại số ứng dụng các phương pháp đại số để nghiên cứu tính chất và quan hệ giữa các số nguyên. Các biểu thức đại số được sử dụng để mô tả các luật tổng quát, như định lý lớn Fermat, và cấu trúc đại số được dùng để phân tích dáng điệu của các số, ví dụ như vành số nguyên.

Ứng Dụng Đại Số Trong Khoa Học và Kỹ Thuật

Ngoài toán học, đại số còn đóng vai trò quan trọng trong nhiều lĩnh vực khoa học tự nhiên, kinh tế, kỹ thuật và khoa học máy tính.

Khoa Học Tự Nhiên

Đại số được sử dụng để diễn đạt các định luật và giải phương trình trong vật lý, hóa học và sinh học.

Kinh Tế, Địa Lý, Kỹ Thuật

Các lĩnh vực này ứng dụng đại số để diễn đạt mối quan hệ, giải quyết vấn đề và mô hình hóa hệ thống.

Trí Tuệ Nhân Tạo và Học Máy

Đại số tuyến tính đóng vai trò quan trọng trong trí tuệ nhân tạo và học máy, cho phép xử lý và phân tích các tập dữ liệu lớn một cách hiệu quả.

Các Lĩnh Vực Chuyên Sâu Khác

Các môn khoa học vật lý như tinh thể học và cơ học lượng tử áp dụng lý thuyết nhóm. Lý thuyết nhóm cũng được ứng dụng để nghiên cứu các câu đố như Sudoku, lập phương Rubik và origami. Lý thuyết mã hóa và mật mã học dựa vào đại số trừu tượng để bảo mật dữ liệu.

Một yếu tố bất ngờ: Việc giải một khối Rubik, tưởng chừng như chỉ là một trò chơi, thực chất lại liên quan đến một cấu trúc đại số phức tạp được gọi là nhóm lập phương Rubik. Các hoán vị của các mặt khối Rubik tạo thành một nhóm, và việc giải khối Rubik có thể được xem là tìm kiếm một chuỗi các phép toán trong nhóm này để đưa khối Rubik về trạng thái ban đầu.

Giáo dục đại số: Từ cán cân đến không gian vectơ

Đại số, một nhánh quan trọng của toán học, thường được tiếp cận thông qua các khái niệm trừu tượng. Tuy nhiên, cách tiếp cận này có thể gây khó khăn cho học sinh, đặc biệt là ở những giai đoạn đầu học tập. Để giúp học sinh nắm bắt những nguyên tắc cơ bản, giáo dục đại số đã và đang sử dụng nhiều công cụ trực quan, trong đó có hình ảnh quen thuộc của một chiếc cân.

Cán cân và phương trình đại số

Trong giảng dạy đại số sơ cấp, cán cân được sử dụng như một mô hình minh họa cho việc giải phương trình. Khối lượng chưa biết trên cân đại diện cho biến số. Việc giải phương trình tương ứng với việc thêm hoặc bớt các vật có khối lượng tương đương ở cả hai bên cân để duy trì sự cân bằng, cho đến khi chỉ còn lại biến số ở một bên, từ đó xác định được giá trị của nó. Phương pháp này giúp học sinh hình dung rõ hơn về các phép toán và quy tắc biến đổi phương trình.

Ứng dụng đại số vào thực tế

Ngoài mô hình cân, bài toán có lời văn cũng là một công cụ hữu ích để minh họa ứng dụng thực tế của đại số. Ví dụ, một bài toán có thể mô tả tình huống anh em nhà A có tổng cộng 12 quả táo, trong đó số táo của em trai gấp đôi số táo của A. Học sinh sẽ cần xây dựng phương trình đại số (2x + x = 12) để biểu diễn tình huống này và tìm ra số táo của A (x = 4). Cách tiếp cận này giúp học sinh thấy được tính ứng dụng của đại số trong đời sống hàng ngày.

Từ đại số sơ cấp đến đại số nâng cao

Ở cấp độ trung học, đại số sơ cấp (thường được gọi là "đại số trường học" ở các nước nói tiếng Anh) là nền tảng để học sinh làm quen với ký hiệu toán học và các khái niệm trừu tượng. Để thành thạo đại số sơ cấp, học sinh cần có kiến thức vững chắc về số học và khả năng tư duy trừu tượng.

Khi bước lên giảng đường đại học, sinh viên ngành toán sẽ tiếp cận với các chủ đề đại số nâng cao hơn như đại số tuyến tính và đại số trừu tượng. Đại số tuyến tính tập trung vào ma trận, không gian vectơ và ánh xạ tuyến tính, trong khi đại số trừu tượng nghiên cứu các cấu trúc đại số như nhóm, trường và vành, cũng như mối quan hệ giữa chúng. Chương trình học cũng thường bao gồm các ví dụ cụ thể về các cấu trúc đại số như hệ thống số hữu tỉ, số thực và đa thức.

Việc học đại số không chỉ cung cấp cho học sinh và sinh viên những công cụ toán học cần thiết mà còn rèn luyện tư duy logic, khả năng giải quyết vấn đề và sự sáng tạo.