Doanh Nghiệp Nhỏ & Thống Kê: Cách Phân Tích Dữ Liệu Đơn Giản Không Ngờ | scantruyen.com

Sự Phát Triển Của Khoa Học Dữ Liệu Và Vai Trò Của Chuyên Gia Không Chuyên

Bối cảnh phân tích và khoa học dữ liệu đã phát triển mạnh mẽ theo thời gian, kéo theo sự thay đổi đa dạng trong các loại hình nhà khoa học dữ liệu. Trong số đó, có một nhóm người đặc biệt – những người có thể không tự nhận mình là nhà khoa học dữ liệu công dân – nhưng lại cực kỳ thành thạo trong việc xử lý dữ liệu, giải quyết vấn đề và đưa ra những hiểu biết kinh doanh giá trị. Những chuyên gia không chuyên về dữ liệu này sử dụng các công cụ và kỹ thuật phân tích dữ liệu hiệu quả để khai thác thông tin chi tiết từ dữ liệu.

Tại Sao Chuyên Gia Kinh Doanh Cần Kiến Thức Thống Kê Và Xác Suất Trong Phân Tích Dữ Liệu?

Có lẽ bạn tự hỏi, tại sao một người trong nhóm này – dù là nhà phân tích dữ liệu, người giải quyết vấn đề dựa trên dữ liệu, hay các chuyên gia kinh doanh khác – lại cần quan tâm đến việc tìm hiểu về thống kê và xác suất để phân tích dữ liệu (và xa hơn là khoa học dữ liệu)? Lý do rất đơn giản: kiến thức này giúp họ nắm vững các khái niệm thống kê cơ bản quan trọng và biết khi nào nên áp dụng chúng.

Hơn nữa, dù có trở thành nhà khoa học dữ liệu "chính thức" hay không, việc trang bị kiến thức này mang lại nhiều lợi ích thiết thực:

• Thay đổi tư duy: Dạy họ cách suy nghĩ khác biệt và mang đến góc nhìn mới mẻ cho các dự án phân tích hoặc dữ liệu của họ.
• Ra quyết định thông minh hơn: Giúp họ đặt những câu hỏi đúng trọng tâm, từ đó đưa ra các quyết định sáng suốt và hiệu quả hơn.
• Phương pháp giải quyết vấn đề tối ưu: Cung cấp một phương pháp tiếp cận khác để giải quyết cùng một vấn đề, có thể cho phép họ bỏ qua những lần thử và sai không cần thiết.

Với mục tiêu giúp các chuyên gia không chuyên về kỹ thuật dễ dàng tiếp cận chủ đề này, phần mới nhất trong loạt bài viết trên blog "In Plain English" của chúng tôi sẽ cung cấp một tổng quan đơn giản về các khái niệm thống kê và xác suất quan trọng cho phân tích dữ liệu và khoa học dữ liệu.

Toán học

Giới thiệu các khái niệm thống kê và xác suất quan trọng

Thống kê, theo định nghĩa, là một khoa học chuyên về việc thu thập, phân tích, trình bày và diễn giải dữ liệu. Với vai trò này, thống kê trở thành một công cụ cực kỳ giá trị cho các chuyên gia giải quyết vấn đề dựa trên dữ liệu. Những người này thường xuyên phải thu thập, làm sạch, chuẩn bị và phân tích một lượng lớn dữ liệu, bao gồm cả dữ liệu có cấu trúc và phi cấu trúc, sau đó truyền đạt những phát hiện quan trọng của mình.

Hai loại thống kê chính: Mô tả và Suy luận

Có hai nhánh chính của thống kê là thống kê mô tả và thống kê suy luận.

Thống kê mô tả

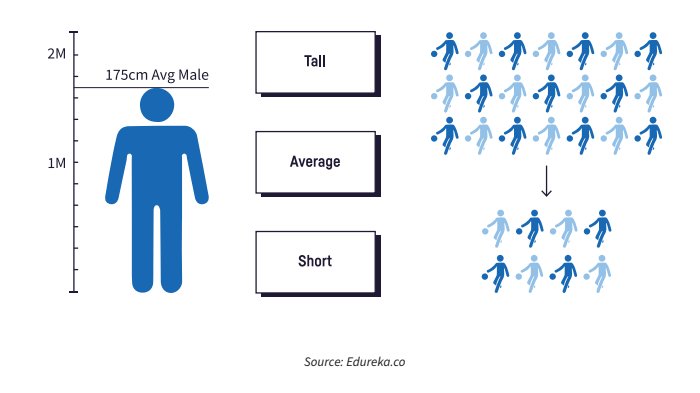
Thống kê mô tả, đúng như tên gọi, tập trung vào việc mô tả các đặc điểm và tính chất quan trọng của dữ liệu nhằm mục đích sắp xếp và tổng hợp thông tin. Chẳng hạn, khi muốn xác định chiều cao trung bình của các cầu thủ trong một đội bóng rổ, bạn sẽ ghi nhận chiều cao của từng cầu thủ, sau đó tính toán chiều cao tối đa, tối thiểu và chiều cao trung bình của toàn đội. Nhờ đó, thống kê mô tả giúp cung cấp cái nhìn tổng quan và trình bày dữ liệu một cách có ý nghĩa.

Thống kê suy luận

Ngược lại, thống kê suy luận cho phép bạn từ một đặc tính quan sát được trong một tập dữ liệu mẫu để suy ra rằng đặc tính tương tự cũng tồn tại trong toàn bộ quần thể mà mẫu đó đại diện. Về bản chất, lý thuyết xác suất được áp dụng để đưa ra những kết luận đáng tin cậy về một quần thể lớn, ngay cả khi bạn chỉ có trong tay dữ liệu từ một mẫu nhỏ. Ví dụ điển hình là việc sử dụng chiều cao trung bình của các cầu thủ trong một đội bóng rổ mẫu để ước lượng chiều cao trung bình của tất cả các cầu thủ bóng rổ.

14 Thuật Ngữ Cơ Bản Về Thống Kê Và Xác Suất

Thống kê và xác suất là nền tảng của phân tích dữ liệu và học máy. Để giúp bạn nắm vững các khái niệm cốt lõi, bài viết này tổng hợp 14 thuật ngữ cơ bản thường gặp. Cho dù bạn là người mới bắt đầu hay muốn ôn lại kiến thức, những định nghĩa rõ ràng dưới đây sẽ vô cùng hữu ích trong công việc và học tập.

Các Thuật Ngữ Thống Kê Và Xác Suất Quan Trọng

• Dân số (Population): Tập hợp các nguồn dữ liệu cần được thu thập. Nó bao gồm một số tham số như trung bình, trung vị, mốt, v.v.
• Mẫu (Sample): Một tập hợp con ngẫu nhiên của quần thể. Có thể dùng để ước tính các tham số của toàn bộ quần thể.
• Biến (Variable): Bất kỳ đặc điểm, số lượng hoặc số lượng nào có thể đo lường hoặc đếm được.
• Tham số (Parameter): Một đại lượng biểu thị một họ phân phối xác suất (tức là giá trị trung bình hoặc trung vị của một quần thể). Tham số là những con số tóm tắt dữ liệu của toàn bộ quần thể, trong khi thống kê là những con số tóm tắt dữ liệu của một mẫu quần thể.
• Sự hồi quy (Regression): Một phương pháp dự đoán có đầu ra là một số thực, tức là một giá trị biểu thị một lượng dọc theo một đường thẳng.
• Xác suất (Probability): Một thước đo số về khả năng xảy ra của một sự kiện cụ thể. Xác suất sử dụng thang điểm từ 0 đến 1, với các giá trị gần 0 biểu thị sự kiện không có khả năng xảy ra và các giá trị gần 1 biểu thị sự kiện có khả năng xảy ra.
• Phân phối xác suất (Probability Distribution): Một hàm mô tả các giá trị và khả năng một biến có thể nhận được trong một phạm vi nhất định.
• Phân phối mẫu (Sampling Distribution): Phân phối xác suất cho thống kê mẫu thu được từ một số mẫu được rút ra từ một quần thể cụ thể.
• Kiểm định giả thuyết (Hypothesis Testing): Một phương pháp để kiểm tra độ chính xác của một mô hình dựa trên một tập dữ liệu trong việc dự đoán bản chất của các tập dữ liệu khác được tạo ra bằng cùng một quy trình.
• Ý nghĩa thống kê (Statistical Significance): Trong thử nghiệm giả thuyết, một kết quả được cho là có ý nghĩa thống kê hoặc có ý nghĩa về mặt thống kê nếu mối quan hệ giữa hai hoặc nhiều biến là do nguyên nhân khác ngoài ngẫu nhiên.
• Giả thuyết không (Null Hypothesis): Một phát biểu chung khẳng định rằng không có mối quan hệ nào giữa hai hiện tượng đang được xem xét hoặc không có liên hệ nào giữa hai nhóm. Nó được ký hiệu là H0 và tin rằng kết quả là kết quả của sự ngẫu nhiên.
• Giả thuyết thay thế (Alternative Hypothesis): Một phát biểu mô tả mối quan hệ giữa hai biến được chọn. Phát biểu này được ký hiệu là H1 hoặc Ha và tin rằng kết quả là kết quả của những nguyên nhân thực sự.
• Giá trị P (P-value): Một thước đo xác suất tìm thấy kết quả quan sát được khi giả thuyết không là đúng.
• Tư duy Bayesian (Bayesian Thinking): Quá trình cập nhật niềm tin khi dữ liệu bổ sung được thu thập. Nó cho thấy chúng ta có thể học hỏi từ dữ liệu bị thiếu, dữ liệu không đầy đủ và các phép tính gần đúng.

Nâng Cao Trình Độ: Ứng Dụng Thống Kê Trong Khoa Học Dữ liệu

Khi bạn sẵn sàng tiến xa hơn và muốn áp dụng sâu rộng thống kê vào lĩnh vực khoa học dữ liệu, việc hiểu rõ mối liên hệ giữa hai ngành này là vô cùng quan trọng. Thống kê và khoa học dữ liệu có sự gắn kết chặt chẽ nhưng vẫn là những thực thể riêng biệt. Cả hai lĩnh vực đều sử dụng một tập dữ liệu nhất định để đưa ra các quan sát và rút ra kết luận về thế giới xung quanh.

Trong thống kê, mục tiêu chính là hiểu rõ mối tương quan giữa các yếu tố đầu vào và kết quả được quan sát. Ngược lại, khoa học dữ liệu tập trung nhiều hơn vào việc thu thập dữ liệu, thiết kế các thử nghiệm dựa trên dữ liệu, sau đó áp dụng thống kê và học máy (ML) để khai thác thông tin từ dữ liệu đó.

Thống Kê Là Nền Tảng Trước Mọi Vấn Đề Khoa Học Dữ liệu

Mặc dù bản chất các câu hỏi đặt ra trong thống kê và khoa học dữ liệu có thể khác nhau, thống kê vẫn luôn là công cụ cần thiết trước khi giải quyết bất kỳ vấn đề khoa học dữ liệu nào. Nhiều người thường vội vàng lao vào học máy mà bỏ qua các bước nền tảng cơ bản. Nguyên tắc Pareto cũng có thể áp dụng ở đây: bạn thường có thể đạt được 80% kết quả chỉ với 20% công cụ. Một nền tảng thống kê vững chắc có thể giúp đơn giản hóa mọi thứ một cách đáng kể.

Ứng Dụng Thống Kê Trong Tác Vụ Khoa Học Dữ liệu Hàng Ngày

Hãy xem xét ví dụ khi bạn đang thử nghiệm nhiều mô hình học máy cho một trường hợp sử dụng cụ thể của khách hàng. Một số mô hình ML yêu cầu các phân phối xác suất cụ thể (tức là các giá trị và khả năng mà một biến có thể nhận trong một phạm vi nhất định) của dữ liệu đầu vào. Do đó, một phần công việc của bạn là phải có khả năng xác định các phân phối này và điều chỉnh dữ liệu đầu vào cho phù hợp. Đây chỉ là một ví dụ nhỏ minh họa cách thống kê được tích hợp vào các tác vụ khoa học dữ liệu hàng ngày.

Xác Định Sự Khác Biệt Giữa Kết Quả Đáng Tin Cậy Và Ngẫu Nhiên

Kiến thức thống kê giúp bạn phân biệt rõ ràng giữa kết quả thực sự đáng tin cậy và những kết quả có khả năng xảy ra do ngẫu nhiên. Giống như bạn đã quen thuộc với phân tích, mọi dự án khoa học dữ liệu đều bắt đầu với một giai đoạn phân tích dữ liệu thăm dò (EDA) để hiểu rõ dữ liệu mà bạn sẽ làm việc. EDA bao gồm tóm tắt và mô tả các mẫu dữ liệu, cả về mặt số liệu và trực quan.

Trích Xuất Giá Trị Và Thông Tin Chi Tiết Từ Dữ liệu

Thường thì các nhà khoa học dữ liệu (và khách hàng của họ) có rất nhiều dữ liệu nhưng lại không biết nên đặt câu hỏi nào hoặc bắt đầu từ đâu để trích xuất giá trị. Thống kê có thể giúp bạn thiết lập một nền tảng vững chắc và định hướng trong việc xác định các mô hình cũng như thông tin chi tiết quan trọng. Theo một cách nào đó, các mô hình học máy thường đặt ra các câu hỏi thống kê đơn giản cho dữ liệu của bạn nhiều lần, sau đó sử dụng các câu trả lời đó để tổng hợp lại, từ đó đưa ra dự đoán hoặc khám phá cấu trúc tổng thể.

Cân Bằng Giữa Khả Năng Diễn Giải Và Độ Chính Xác Trong AI/ML

Ngày nay, các nhà khoa học dữ liệu sử dụng mô hình học máy và hệ thống AI đang đối mặt với một thách thức lớn trong việc cân bằng giữa khả năng diễn giải và độ chính xác. Điều này xuất phát từ sự khác biệt cơ bản giữa mô hình hộp đen và mô hình hộp trắng. Trong AI và ML, bạn thường tập trung vào việc xác định độ chính xác hoặc khả năng dự đoán (cho ra một con số hoặc giá trị). Ngược lại, thống kê giúp bạn diễn giải ý nghĩa của kết quả đó và mô tả nguồn gốc của nhãn. Thống kê cung cấp thêm một lớp diễn giải, từ đó củng cố lý do tại sao bạn tin vào một kết quả cụ thể.