Lý thuyết đồ thị: Giải mã thế giới quanh ta từ mạng xã hội đến lộ trình giao thông | scantruyen.com

Kính thưa quý vị độc giả, những tâm hồn yêu toán và đam mê khám phá thế giới qua lăng kính của logic! Hôm nay, chúng ta sẽ cùng nhau dấn bước vào một trong những lĩnh vực toán học hấp dẫn và ứng dụng bậc nhất: Lý thuyết đồ thị. Đây không chỉ là một nhánh tri thức sâu sắc mà còn là một công cụ phân tích sắc bén, giúp chúng ta nhìn thấu và đơn giản hóa những cấu trúc phức tạp nhất, từ mạng lưới liên kết xã hội cho đến các hệ thống hậu cần tinh vi.

Về bản chất, lý thuyết đồ thị là nghiên cứu chuyên sâu về cấu trúc dữ liệu đồ thị. Tại đây, mọi mối quan hệ, mọi tương tác giữa các đối tượng đều được mô hình hóa một cách tinh tế bằng các đỉnh (hay còn gọi là nút) được kết nối bởi những cạnh. Từ bố cục thành phố tấp nập đến luồng dữ liệu khổng lồ trong hệ thống máy tính, hoặc thậm chí là một tập hợp các điểm đến và tuyến đường, đồ thị đều cho phép chúng ta trừu tượng hóa, định lượng và đơn giản hóa bức tranh toàn cảnh của một hệ thống động phức tạp.

Lịch sử của lĩnh vực này đã khởi nguồn từ thế kỷ 18, khi nhà toán học vĩ đại Leonhard Euler đặt viên gạch đầu tiên qua công trình giải quyết bài toán Bảy cây cầu ở Königsberg. Kể từ đó, lý thuyết đồ thị đã không ngừng phát triển, trở thành nền tảng không thể thiếu cho nhiều ứng dụng then chốt ngày nay, từ tối ưu hóa mạng, thuật toán xếp hạng trong công cụ tìm kiếm cho đến các hệ thống định tuyến GPS mà chúng ta sử dụng hàng ngày.

Tóm tắt: Lý thuyết đồ thị nghiên cứu cấu trúc dữ liệu đồ thị và mối quan hệ giữa các đối tượng sử dụng đỉnh và cạnh. Xuất phát từ công trình của Leonhard Euler về bài toán Bảy cây cầu ở Königsberg, lý thuyết đồ thị có ứng dụng trong tối ưu hóa mạng, công cụ tìm kiếm và định tuyến.

Lý thuyết đồ thị: Từ khái niệm đến sức hút ứng dụng

Thoạt nghe, "Lý thuyết đồ thị" có thể gợi lên hình ảnh của những khái niệm trừu tượng và khô khan. Tuy nhiên, tôi xin khẳng định rằng đây là một lĩnh vực chứa đựng vô vàn ứng dụng thực tiễn, đầy bất ngờ và hữu ích. Trong bài viết này, chúng ta sẽ không đi sâu vào chi tiết hàn lâm, mà tập trung vào việc khám phá sức mạnh ứng dụng của nó, với hy vọng thuyết phục bạn rằng việc trang bị những kiến thức cơ bản về lý thuyết đồ thị chính là chìa khóa để giải quyết nhiều bài toán thú vị bạn có thể gặp phải.

Vậy, chính xác thì lý thuyết đồ thị là gì? Nó là khoa học nghiên cứu về cấu trúc dữ liệu đồ thị, nơi các mối quan hệ giữa các đối tượng được biểu diễn một cách trực quan qua các đỉnh (hay nút) và cạnh. Với khả năng trừu tượng hóa mọi thứ – từ sơ đồ giao thông đô thị đến cấu trúc phức tạp của dữ liệu máy tính – lý thuyết đồ thị cung cấp một công cụ vô giá để định lượng và đơn giản hóa các thành phần chuyển động trong một hệ thống động. Nhờ đó, chúng ta có thể phân tích và tìm ra những tuyến đường hoặc kết nối tối ưu nhất.

Sức ảnh hưởng của đồ thị đã ăn sâu vào cuộc sống số hiện đại. Hãy nghĩ về cách các mạng xã hội kết nối hàng tỷ người, cách thuật toán xếp hạng siêu liên kết định hình kết quả của các công cụ tìm kiếm, hay cách hệ thống bản đồ GPS chỉ dẫn bạn con đường ngắn nhất về nhà. Tất cả đều là những ví dụ điển hình, minh chứng rõ ràng cho vai trò không thể thiếu của lý thuyết đồ thị.

Hành trình tối ưu hóa kho hàng: Một ví dụ thực tế

Để minh họa rõ hơn về sức mạnh thực tiễn của lý thuyết đồ thị, tôi muốn cùng bạn khám phá một ví dụ cụ thể: bài toán lập kế hoạch và tối ưu hóa lộ trình trong một nhà kho lớn. Hãy tưởng tượng một nhà kho rộng lớn với hàng ngàn mặt hàng khác nhau được đặt rải rác tại nhiều điểm nhận hàng. Thử thách đặt ra là: với một danh sách các mặt hàng cần thu thập, làm thế nào để xây dựng một lộ trình di chuyển hiệu quả nhất qua nhà kho, sao cho tổng quãng đường là tối thiểu?

Đối với những nhà nghiên cứu hay chuyên gia đã quen thuộc với lĩnh vực này, bài toán trên hẳn sẽ gợi nhắc ngay đến bài toán người bán hàng du lịch (Traveling Salesperson Problem - TSP) nổi tiếng. TSP không chỉ là một trong những bài toán kinh điển và thách thức nhất trong tối ưu hóa tổ hợp, mà còn đóng vai trò trụ cột trong khoa học máy tính lý thuyết và nghiên cứu vận hành. Nó thách thức chúng ta tìm ra con đường ngắn nhất đi qua một tập hợp các điểm và quay trở lại điểm xuất phát, mỗi điểm chỉ được ghé thăm một lần.

Mục tiêu của tôi trong bài viết này không phải là cung cấp một bản giới thiệu toàn diện về lý thuyết đồ thị – một nhiệm vụ đồ sộ và cần nhiều thời gian hơn. Thay vào đó, qua ví dụ thực tế về tối ưu hóa kho hàng này, tôi hy vọng có thể truyền cảm hứng và thuyết phục bạn rằng, việc trang bị những kiến thức cơ bản về lý thuyết đồ thị thực sự rất hữu ích và có thể mở ra những hướng giải quyết sáng tạo cho nhiều vấn đề phức tạp trong công việc và cuộc sống.

Để hoàn thiện bức tranh, chúng ta sẽ bắt đầu với một cái nhìn tổng quan lịch sử về sự ra đời của lĩnh vực này, đồng thời nhấn mạnh tầm quan trọng và phạm vi ứng dụng rộng lớn của nó trong nhiều lĩnh vực đa dạng. Sau phần giới thiệu này, trọng tâm sẽ được chuyển về ví dụ tối ưu hóa kho hàng đã bàn luận ở trên, nơi chúng ta sẽ khám phá cách áp dụng lý thuyết đồ thị để tìm ra giải pháp tối ưu.

Toán

Khám phá Lịch sử Lý thuyết Đồ thị: Hành trình từ bảy cây cầu Königsberg đến thế giới hiện đại

Hãy cùng ngược dòng thời gian về thế kỷ 18, tại thành phố Königsberg cổ kính, nay là Kaliningrad của Nga. Tại đây, một câu đố tưởng chừng đơn giản về những cây cầu bắc qua sông Pregel đã khơi nguồn cảm hứng cho một trong những lĩnh vực toán học hấp dẫn và ứng dụng rộng rãi nhất hiện nay: Lý thuyết Đồ thị. Chính nhà toán học vĩ đại người Thụy Sĩ Leonhard Euler đã đặt viên gạch đầu tiên, khai sinh ra một công cụ phân tích quyền năng mà chúng ta vẫn đang khám phá và ứng dụng.

Bí ẩn của Bảy cây cầu Königsberg: Khởi nguyên của một lý thuyết

Königsberg nổi tiếng với địa thế độc đáo, được dòng sông Pregel chia cắt thành hai bờ và hai hòn đảo lớn mang tên Kneiphof và Lomse. Tổng cộng có bảy cây cầu nối liền các khu vực đất liền và đảo này, tạo thành một mạng lưới giao thông đặc trưng. Vấn đề đặt ra là liệu có thể tìm được một lộ trình đi bộ xuyên thành phố sao cho mỗi cây cầu chỉ được đi qua đúng một lần duy nhất hay không? Đây không chỉ là một trò chơi giải đố mà còn là thách thức lớn đối với trí tuệ thời bấy giờ.

Thiên tài Euler và phép trừu tượng hóa đột phá

Bằng nhãn quan sắc bén của một học giả toán học lỗi lạc, Leonhard Euler đã nhìn thấu bản chất của bài toán. Ông nhận ra rằng chìa khóa không nằm ở hình dạng cụ thể của các vùng đất hay kiến trúc của từng cây cầu, mà ở mối quan hệ kết nối giữa chúng. Từ đó, Euler đã thực hiện một bước nhảy vọt trong tư duy: ông trừu tượng hóa các vùng đất thành các đỉnh (hoặc nút) và các cây cầu thành các cạnh nối các đỉnh đó lại với nhau. Đây chính là biểu diễn trực quan đầu tiên của một đồ thị hiện đại.

Trong Lý thuyết Đồ thị, một đồ thị được định nghĩa là một tập hợp các điểm, gọi là đỉnh (vertices) hoặc nút (nodes), được kết nối với nhau bởi một tập hợp các đường, gọi là cạnh (edges). Sự trừu tượng hóa kỳ diệu này đã biến một câu đố địa lý phức tạp thành một mô hình toán học đơn giản, chỉ tập trung vào những thông tin cốt yếu để giải quyết vấn đề, giúp việc phân tích trở nên khả thi về mặt toán học.

Kết quả bất ngờ và di sản vượt thời gian

Với phương pháp phân tích mà mình đã phát triển, Euler đã chứng minh một cách chặt chẽ rằng bài toán Bảy cây cầu ở Königsberg thực sự không có lời giải. Không thể nào đi qua mỗi cây cầu chỉ một lần. Tuy nhiên, thành tựu vĩ đại của ông không chỉ nằm ở kết luận này, mà còn ở việc ông đã kiến tạo một kỹ thuật phân tích phù hợp, một khung lý thuyết mới mẻ để giải quyết các vấn đề tương tự. Công trình của ông đã đặt nền móng vững chắc, và từ đó, Lý thuyết Đồ thị đã chứng kiến những bước phát triển ổn định, liên tục trong suốt thế kỷ 19 và 20.

Ngày nay, từ một bài toán vui ở một thành phố nhỏ bé, Lý thuyết Đồ thị đã vươn mình trở thành một công cụ không thể thiếu với vô vàn ứng dụng rộng rãi. Chúng ta có thể thấy nó trong khoa học máy tính với mạng internet và thuật toán tìm đường, trong quy hoạch giao thông, trong phân tích mạng lưới xã hội, cho đến những lĩnh vực tưởng chừng xa lạ như sinh học phân tử hay kinh tế học. Di sản của Euler vẫn sống mãi, tiếp tục định hình và giải quyết những thách thức phức tạp của thế giới hiện đại.

Lý Thuyết Đồ Thị: Nền Tảng Và Ứng Dụng Trong Thế Giới Thực

Chào mừng quý vị đến với thế giới đầy mê hoặc của lý thuyết đồ thị! Để thấu hiểu cách thức những cấu trúc toán học này được ứng dụng vào thực tiễn, chúng ta hãy cùng nhau điểm qua vài kiến thức cơ bản về các loại đồ thị khác nhau. Đây sẽ là nền tảng vững chắc cho ví dụ về tối ưu hóa đường đi mà chúng ta sẽ cùng khám phá sau đây.

Sức Mạnh Của Lý Thuyết Đồ Thị: Định Lượng Mối Quan Hệ

Lý thuyết đồ thị, với bản chất là công cụ nghiên cứu các mối quan hệ, mang lại một phương pháp vô cùng hữu ích để định lượng và đơn giản hóa các thành phần phức tạp trong những hệ thống động. Việc phân tích các cấu trúc đồ thị mở ra cánh cửa dẫn đến lời giải cho vô vàn vấn đề hóc búa, từ việc sắp xếp, kết nối mạng, cho đến tối ưu hóa, ghép nối và vận hành các hệ thống.

Những Ứng Dụng Đa Dạng Của Đồ Thị Trong Đời Sống

Đồ thị có khả năng mô hình hóa rất nhiều loại mối quan hệ và quy trình trong các hệ thống vật lý, sinh học, xã hội và thông tin. Những ứng dụng thực tiễn của chúng trải dài trên nhiều lĩnh vực, mang lại lợi ích không ngờ:

• Tìm kiếm các cộng đồng trong mạng lưới rộng lớn, chẳng hạn như đề xuất bạn bè/kết nối trên mạng xã hội, hay theo dõi khả năng lây lan của COVID-19 trong cộng đồng qua các mối liên hệ.
• Xếp hạng các siêu liên kết, một yếu tố then chốt giúp các công cụ tìm kiếm hoạt động hiệu quả.
• Hệ thống GPS trong Google Maps, giúp chúng ta tìm ra con đường ngắn nhất để về nhà hay đến bất kỳ địa điểm nào.
• Nghiên cứu sâu sắc về phân tử và nguyên tử trong lĩnh vực hóa học.
• Giải trình tự DNA, mở khóa những bí ẩn của di truyền học.
• Đảm bảo an ninh cho mạng máy tính, bảo vệ dữ liệu và thông tin quan trọng.

Minh Họa Trực Quan: Đồ Thị Trong Thực Tế

Để dễ hình dung hơn về lý thuyết này, hãy cùng xem xét một số minh họa cụ thể về đồ thị:

• Chúng ta có thể hình dung một ví dụ đơn giản là đồ thị chỉ với sáu nút, đại diện cho sáu thực thể và các mối quan hệ trực tiếp giữa chúng.
• Hay phức tạp hơn là một mạng xã hội, nơi mỗi nút là một người dùng và các cạnh thể hiện mối quan hệ kết nối giữa họ.

Đa Dạng Các Loại Đồ Thị

Điều thú vị là, có rất nhiều loại đồ thị khác nhau, mỗi loại được thiết kế để mô tả những dạng vấn đề riêng biệt và những ràng buộc đặc thù trong từng ngữ cảnh. Sự đa dạng này chính là chìa khóa để lý thuyết đồ thị có thể giải quyết một phổ rộng các thách thức.

Chào mừng quý vị độc giả yêu toán đến với thế giới đầy mê hoặc của lý thuyết đồ thị! Trong vô vàn khái niệm toán học, đồ thị nổi lên như một công cụ mạnh mẽ, giúp chúng ta mô hình hóa và giải quyết vô số vấn đề thực tiễn, từ mạng xã hội cho đến quy hoạch đô thị. Tuy nhiên, để thực sự làm chủ nghệ thuật này, bước đầu tiên và quan trọng nhất là phải nắm rõ các loại đồ thị khác nhau. Bởi lẽ, mỗi loại đồ thị lại mang trong mình những đặc tính riêng, quyết định cách chúng ta tiếp cận và tìm lời giải cho bài toán. Vậy, hãy cùng tôi khám phá ba loại đồ thị cơ bản mà bất kỳ ai muốn dấn thân vào lĩnh vực này đều cần phải biết.

Khám phá Các Loại Đồ Thị Cơ Bản trong Lý Thuyết Đồ Thị

Khi bước chân vào thế giới của lý thuyết đồ thị, chúng ta sẽ bắt gặp nhiều cách biểu diễn đồ thị khác nhau. Việc xác định đúng loại đồ thị mình đang làm việc là chìa khóa để giải quyết bài toán hiệu quả. Dưới đây là ba loại đồ thị quan trọng mà bạn cần nắm vững:

• Đồ thị vô hướng: Mọi đường dẫn giữa các nút đều là song hướng, có nghĩa là bạn có thể di chuyển theo cả hai chiều.
• Đồ thị có hướng (Digraph): Các đường đi giữa các nút có một hướng xác định, không nhất thiết là hai chiều.
• Đồ thị có trọng số: Ngoài hướng (hoặc không), các đường dẫn còn được gán thêm trọng số để biểu thị các giá trị như khoảng cách, chi phí hay thời gian.

1. Đồ Thị Vô Hướng: Kết Nối Hai Chiều

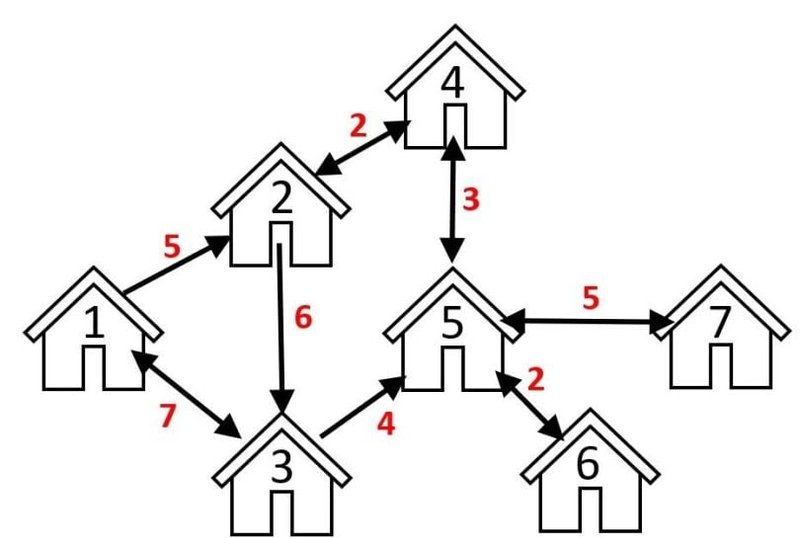
Hãy tưởng tượng bạn đang xem bản đồ một thành phố, nơi mỗi nút biểu diễn một ngôi nhà tại các vị trí khác nhau, và mỗi cạnh là con đường nối giữa chúng. Trong một đồ thị vô hướng, như chính tên gọi của nó, không có sự phân biệt về hướng di chuyển trên các con đường này. Điều đó có nghĩa là, nếu có một con đường nối nhà số 1 với nhà số 2, bạn hoàn toàn có thể đi từ nhà 1 sang nhà 2 và ngược lại, từ nhà 2 về nhà 1, không chút trở ngại.

Trong ví dụ đơn giản này, chúng ta giả định rằng tất cả các con đường đều là đường hai chiều. Chúng ta không cần phải bận tâm về bất kỳ con đường một chiều nào, mọi kết nối đều là song phương.

2. Đồ Thị Có Hướng (DiGraphs): Lối Đi Một Chiều

Khi chuyển sang đồ thị có hướng, mọi chuyện trở nên thú vị hơn một chút. Lúc này, chúng ta không chỉ quan tâm đến việc các nút có được nối với nhau hay không, mà còn phải xác định rõ hướng của các đường đi đó. Điều này có nghĩa là, nếu có một cạnh hướng từ nút 1 đến nút 2, bạn có thể đi từ 1 đến 2, nhưng chưa chắc đã có thể đi ngược lại từ 2 về 1.

Tiếp tục với ví dụ về các ngôi nhà trong thành phố: nếu có một cạnh có hướng từ nhà 1 đến nhà 2, điều này biểu thị một con đường một chiều. Bạn có thể lái xe từ nhà 1 đến nhà 2, nhưng để trở về nhà 1 từ nhà 2, bạn sẽ phải tìm một tuyến đường khác, ví dụ như từ nhà 2 đi đến nhà 3 rồi mới về nhà 1. Tuy nhiên, nếu giữa nhà 2 và nhà 4 có các mũi tên kép, điều đó cho thấy bạn có thể lái xe an toàn theo cả hai hướng, giống như một con đường hai chiều đặc biệt trong mạng lưới một chiều.

3. Đồ Thị Có Trọng Số: Chi Phí và Khoảng Cách

Trong nhiều ứng dụng thực tế, việc gán thêm một "trọng số" cho các cạnh của đồ thị là vô cùng cần thiết. Trọng số này có thể biểu thị nhiều ý nghĩa khác nhau như chi phí, khoảng cách, thời gian, hoặc thậm chí là lưu lượng giao thông. Đồ thị có trọng số giúp chúng ta mô hình hóa các tình huống phức tạp hơn, nơi mà không phải mọi đường đi đều "ngang giá" nhau.

Một điều thú vị là, đồ thị có trọng số có thể là có hướng hoặc vô hướng. Trở lại với ví dụ về các con đường nối các ngôi nhà trong thành phố, trọng số của các cạnh lúc này có thể biểu diễn khoảng cách lái xe giữa chúng. Giả sử bạn muốn tìm tuyến đường tối ưu nhất từ "Ngôi nhà 1" sang "Ngôi nhà 5" ở bên kia thành phố. Lúc này, bạn không chỉ cần biết những con đường nào có thể đi được (các cạnh), mà còn phải xem xét khoảng cách trên mỗi con đường (trọng số của cạnh).

Trong tình huống này, tuyến đường tối ưu sẽ là từ 1 đến 2, rồi từ 2 đến 4, và cuối cùng từ 4 đến 5. Tổng khoảng cách sẽ là 5 + 2 + 3 = 10. Nếu chọn tuyến đường khác, ví dụ như từ 1 đến 3 rồi từ 3 đến 5, tổng khoảng cách sẽ là 7 + 4 = 11. Rõ ràng, tuyến đường đầu tiên là lựa chọn tốt hơn.

Từ ví dụ đơn giản này, bạn có thể dễ dàng hình dung sức mạnh của đồ thị có trọng số trong việc giải quyết các bài toán thực tế phức tạp. Nó được ứng dụng rộng rãi trong việc lập kế hoạch tuyến đường cho GPS, các công cụ tìm kiếm so sánh thời gian và chi phí chuyến bay, hay thậm chí là tối ưu hóa bố trí mạng lưới đường bộ và cơ sở hạ tầng trong một đô thị.

Bây giờ, chúng ta hãy cùng tập trung vào một ứng dụng cụ thể hơn: lập kế hoạch lộ trình khi lấy hàng trong kho, một bài toán tối ưu hóa quen thuộc.

Khám Phá Sức Mạnh Lý Thuyết Đồ Thị: Tối Ưu Hóa Tuyến Đường Lấy Hàng Trong Kho Hiện Đại

Trong môi trường kho hàng hiện đại, việc tối ưu hóa tuyến đường lấy hàng đóng vai trò then chốt trong hiệu quả hoạt động. Với một danh sách các mặt hàng cần được lấy, bài toán đặt ra cho chúng ta là làm sao tìm được tuyến đường ngắn nhất. Tuyến đường này không chỉ phải đi qua tất cả các điểm lấy hàng được chỉ định mà còn phải tuân thủ nghiêm ngặt các quy tắc di chuyển, đặc biệt là hướng đi và các điểm rẽ được phép trong từng hành lang của kho. Đây là một thách thức thú vị đòi hỏi sự kết hợp giữa logistics và tư duy toán học.

Ứng Dụng Lý Thuyết Đồ Thị: Biến Bài Toán Thành Đồ Thị

Để giải quyết bài toán phức tạp này, chúng ta có thể chuyển hóa nó thành một mô hình tối ưu hóa kinh điển trong lĩnh vực lý thuyết đồ thị. Hãy hình dung mỗi điểm lấy hàng trong kho giờ đây là một "nút" (hay "đỉnh") trên đồ thị của chúng ta. Các tuyến đường, hay những hành lang di chuyển được phép, sẽ trở thành những "cạnh" nối các nút này lại, đồng thời thể hiện khoảng cách giữa chúng. Để mọi thứ trở nên dễ hình dung hơn, chúng ta hãy cùng nhau khám phá một ví dụ nhỏ.

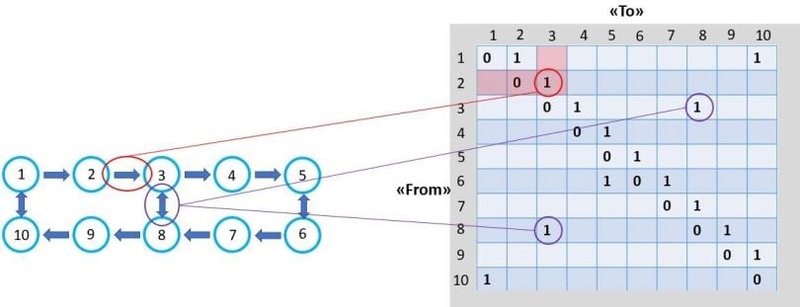
Hãy cùng nhìn vào một biểu đồ minh họa đơn giản. Nó mô tả hai hành lang chính trong kho, mỗi hành lang có năm điểm lấy hàng hay "kệ". Mỗi kệ này được đánh dấu là một nút trên đồ thị, với các địa chỉ từ 1 đến 10. Điều thú vị ở đây là các mũi tên: chúng không chỉ đơn thuần là đường nối, mà còn chỉ ra hướng di chuyển được phép. Một mũi tên đơn nghĩa là chỉ được đi một chiều, trong khi mũi tên kép cho phép chúng ta di chuyển theo cả hai hướng. Khá trực quan phải không nào?

Chính khả năng biểu diễn các quy tắc di chuyển phức tạp này dưới dạng đồ thị đã mở ra cánh cửa cho việc áp dụng những "công cụ" toán học mạnh mẽ từ lý thuyết đồ thị. Chúng ta có thể dùng chúng để "khai quật" tuyến đường lái xe tối ưu nhất giữa các điểm lấy hàng (hay các nút kệ hàng) trong kho của mình.

Ma Trận Kề: Ngôn Ngữ Số Hóa Của Đồ Thị Kho Hàng

Để đưa mô hình này lên một tầm cao toán học, chúng ta có thể sử dụng ma trận kề (adjacency matrix). Ma trận kề là một công cụ cực kỳ hữu hiệu, giúp chúng ta biểu diễn một cách chính xác mọi tuyến đường được phép di chuyển giữa các nút trong đồ thị kho hàng. Nó giống như một "bản đồ" số hóa, ghi lại mọi kết nối khả thi.

Hãy cùng xem xét các ví dụ cụ thể về cách ma trận kề hoạt động:

• Ví dụ 1: Nếu bạn được phép di chuyển từ nút 2 đến nút 3, nhưng chiều ngược lại (từ 3 về 2) thì không, điều này sẽ được thể hiện bằng số "1" tại vị trí tương ứng trong ma trận kề, chỉ rõ kết nối một chiều.
• Ví dụ 2: Ngược lại, nếu việc di chuyển từ nút 8 đến nút 3 và từ nút 3 đến nút 8 đều được phép, thì cả hai vị trí tương ứng trong ma trận kề sẽ đều mang giá trị "1". Điều này cho thấy một kết nối hai chiều, hay nói cách khác, ma trận kề sẽ đối xứng tại các vị trí này khi xét đến hướng di chuyển.

Kính chào quý vị độc giả yêu toán và những ai đang tìm kiếm lời giải cho bài toán tối ưu trong quản lý kho hàng! Hôm nay, chúng ta sẽ cùng nhau khám phá cách mà những nguyên lý toán học tưởng chừng khô khan lại có thể "thắp sáng" con đường hiệu quả nhất trong những mê cung kệ hàng khổng lồ.

Giải Quyết Bài Toán Kho Hàng: Từ Thực Tế Đến Đồ Thị

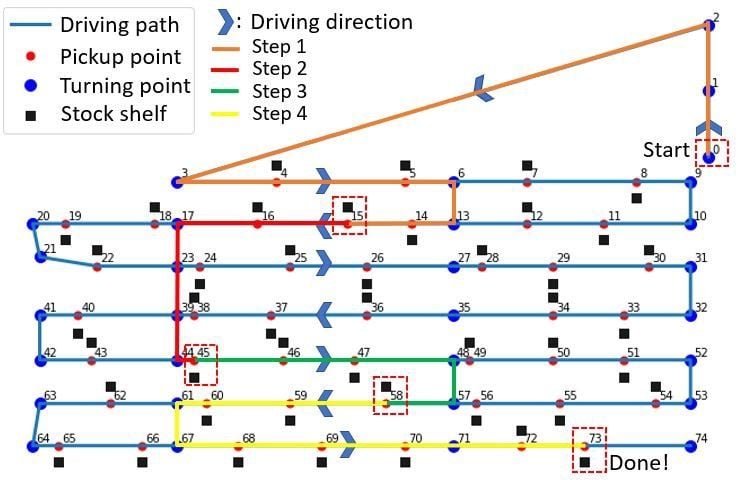
Trở lại với bài toán quản lý kho hàng, nơi mà mỗi bước đi, mỗi quyết định đều ẩn chứa tiềm năng tối ưu hóa. Dù một nhà kho thực tế có thể rộng lớn và phức tạp hơn rất nhiều so với những ví dụ đơn giản, song các nguyên tắc cốt lõi để biến bài toán thực tế thành một mô hình đồ thị vẫn không hề thay đổi. Để dễ hình dung và phù hợp hơn về mặt trực quan cho bài viết này, chúng ta sẽ thu nhỏ tổng số kệ hàng hay còn gọi là các "điểm lấy hàng" xuống còn khoảng 50 kệ. Những điểm này được minh họa bằng các ô vuông đen trong hình ảnh mà chúng ta sẽ cùng xem xét.

Mỗi điểm lấy hàng đều được gán một địa chỉ cụ thể, tương ứng với một số nút, từ 1 đến 74, trong mô hình đồ thị của chúng ta. Không chỉ vậy, những ràng buộc quan trọng khác đã đề cập trước đó, chẳng hạn như hướng di chuyển được phép trong mỗi hành lang, cũng như các "điểm rẽ" chiến lược và những "lối tắt" thông minh giữa các hành lang, cũng được chỉ ra rõ ràng trên biểu đồ.

Biểu đồ biểu diễn kho hàng đơn giản của chúng ta. Ảnh: Vegard Flovik

Đây chính là bức tranh trực quan về biểu đồ biểu diễn kho hàng đơn giản của chúng ta. Nó không chỉ là một hình vẽ mà là một ngôn ngữ toán học giúp chúng ta nhìn nhận cấu trúc kho một cách có hệ thống, đặt nền móng vững chắc cho việc tìm kiếm lộ trình hiệu quả.

Ma Trận Kề: "Bản Đồ" Chi Tiết Của Lộ Trình Tối Ưu Kho Hàng

Sau khi đã có biểu đồ đồ thị trong tay, bước tiến hóa tiếp theo trong hành trình tối ưu hóa chính là chuyển đổi nó thành một ma trận kề. Tại sao lại là ma trận kề? Đơn giản thôi, bởi vì chúng ta không chỉ muốn tìm ra một lộ trình "đúng", mà còn muốn tìm ra lộ trình tối ưu nhất với tổng khoảng cách di chuyển là nhỏ nhất. Để đạt được điều đó, ma trận kề của chúng ta phải bao gồm cả thông tin về khoảng cách lái xe giữa các nút khác nhau.

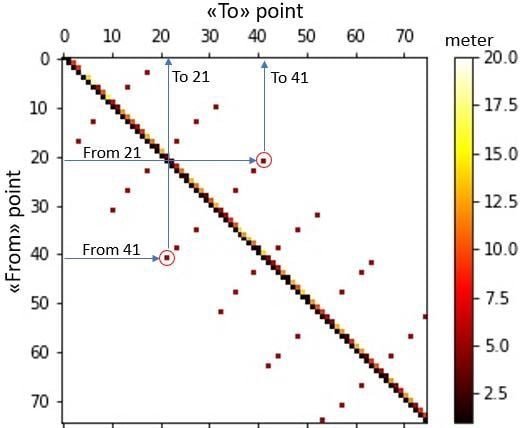
Ma trận kề cho đồ thị kho hàng. Ảnh: Vegard Flovik

Và đây là ma trận kề, "bản đồ" chứa đựng mọi thông tin cần thiết cho đồ thị kho hàng. Từng ô trong ma trận này không chỉ cho chúng ta biết đường nào được phép đi, đường nào không, những "lối tắt" nào có thể tận dụng, hay bất kỳ hạn chế đặc biệt nào khác, mà còn biểu thị khoảng cách lái xe giữa các nút bằng những sắc màu khác nhau. Thử nhìn xem, lối tắt kỳ diệu giữa nút 21 và 41 mà chúng ta đã thấy trên biểu đồ đồ thị cũng hiện diện rõ ràng trong ma trận kề này. Ngược lại, những "vùng trắng" mênh mông trong ma trận chính là lời khẳng định hùng hồn rằng đó là những con đường không được phép, chúng được biểu thị bằng một "khoảng cách vô hạn" giữa các nút đó, ngụ ý không thể di chuyển trực tiếp.

Cách sử dụng lý thuyết đồ thị để tối ưu hóa đường đi

Trong thế giới logistics và quản lý kho bãi hiện đại, việc tối ưu hóa đường đi không chỉ là mong muốn mà còn là yếu tố then chốt quyết định hiệu quả hoạt động. Chỉ đơn thuần biểu diễn trừu tượng một kho hàng dưới dạng đồ thị chưa phải là lời giải. Điều kỳ diệu nằm ở chỗ, khi kho hàng được "phác họa" thành một đồ thị, chúng ta sẽ mở khóa một cánh cửa dẫn đến kho tàng tri thức toán học đồ sộ, sẵn sàng ứng dụng các thuật toán mạnh mẽ từ lý thuyết đồ thị để giải quyết những thách thức thực tế.

Lĩnh vực tối ưu hóa đồ thị từ lâu đã là một "ngôi sao sáng" trong toán học ứng dụng, mang đến vô vàn phương pháp và thuật toán để giải quyết triệt để các bài toán tối ưu. Trong khuôn khổ bài viết này, chúng ta sẽ cùng khám phá sức mạnh của thuật toán Floyd-Warshall – một "công cụ" kinh điển và vô cùng hiệu quả để xác định đường đi ngắn nhất trên đồ thị có trọng số. Điều thú vị là, chỉ với một lần thực thi duy nhất, thuật toán này sẽ hé lộ tổng trọng số (độ dài) của những con đường ngắn nhất giữa mọi cặp nút trong đồ thị. Mặc dù phiên bản cơ bản không trực tiếp cung cấp chi tiết lộ trình, nhưng một biến thể khéo léo sử dụng "ma trận tái tạo đường đi" sẽ giúp chúng ta truy xuất từng bước của hành trình tối ưu đó.

Vậy làm thế nào để ứng dụng? Đơn giản thôi! Khi bạn cung cấp cho thuật toán một "danh sách thứ tự chọn" – tức là một chuỗi các mặt hàng bạn cần thu thập – nó sẽ tức thì tính toán và vạch ra lộ trình tối ưu nhất. Lộ trình này đảm bảo tổng quãng đường di chuyển để lấy tất cả các mặt hàng trong danh sách là nhỏ nhất có thể, giúp tiết kiệm thời gian và công sức đáng kể.

Ví dụ về tối ưu hóa đường đi trong lý thuyết đồ thị

Để trực quan hóa sức mạnh của phương pháp này, hãy cùng xem xét một ví dụ cụ thể. Giả sử chúng ta có một danh sách chọn ngắn gọn: bắt đầu từ nút 0, sau đó lần lượt chọn các mặt hàng tại nút 15, 45, 58 và 73. Hãy tưởng tượng đây là các vị trí trong kho hàng của bạn.

Bằng cách tính toán một "ma trận khoảng cách" – ký hiệu là D – thuật toán sẽ khéo léo xác định tuyến đường ngắn nhất có thể giữa từng cặp điểm trong danh sách chọn. Từ ma trận này, tổng quãng đường di chuyển cần thiết để ghé thăm tất cả các vị trí sẽ được tính toán một cách chính xác.

• Bước 1: Khoảng cách từ D[0] đến D[15] là 90 m
• Bước 2: Khoảng cách từ D[15] đến D[45] là 52 m
• Bước 3: Khoảng cách từ D[45] đến D[58] là 34 m
• Bước 4: Khoảng cách từ D[58] đến D[73] là 92 m

Tổng quãng đường di chuyển tối ưu trong ví dụ này là 268m.

Qua hàng loạt thử nghiệm với nhiều danh sách chọn đầu vào khác nhau, từ việc kiểm tra các tuyến đường đề xuất đến việc xác minh khoảng cách tính toán, thuật toán này đã chứng minh khả năng vượt trội của mình. Nó luôn tìm ra tuyến đường tối ưu trong mọi trường hợp, đồng thời tuân thủ nghiêm ngặt mọi ràng buộc đã định – từ hướng di chuyển cho phép cho đến việc tận dụng mọi "lối tắt" khả thi để giảm thiểu tổng quãng đường một cách hiệu quả nhất.

Khám Phá Sức Mạnh Của Tối Ưu Hóa Đường Dẫn Trong Quản Lý Kho Hàng

Trong thế giới kho hàng năng động ngày nay, việc tối ưu hóa lộ trình di chuyển không chỉ là một ý tưởng hay mà còn là chìa khóa để khai thác những thông tin chi tiết vô giá. Chúng ta hãy cùng khám phá một thuật toán tối ưu hóa mới được phát triển, có khả năng tính toán lộ trình tối ưu nhất qua mọi điểm trên danh sách lệnh lấy hàng trong một môi trường kho hàng đơn giản. Chỉ với việc cung cấp một danh sách các lệnh lấy hàng, chúng ta có thể dễ dàng thu thập những số liệu thống kê quan trọng về quãng đường di chuyển trung bình cho mỗi lệnh. Hơn thế nữa, những số liệu này có thể được lọc sâu hơn dựa trên nhiều tiêu chí như loại mặt hàng, khách hàng hay ngày tháng, mở ra cánh cửa đến những phân tích đầy tiềm năng. Trong bài viết này, tôi sẽ chia sẻ một vài ví dụ điển hình về cách chúng ta có thể trích xuất những thông tin thú vị từ một công cụ tối ưu hóa đường dẫn mạnh mẽ như vậy.

Để minh họa, tôi đã tạo ra một tập dữ liệu gồm 10.000 danh sách lệnh lấy hàng. Mỗi danh sách chứa từ một đến 30 mặt hàng, được bố trí ngẫu nhiên tại các điểm lấy hàng trong kho (từ địa chỉ ba đến 74). Bằng cách áp dụng quy trình tối ưu hóa đường dẫn lên toàn bộ tập dữ liệu này, chúng ta có thể bắt đầu khai thác những số liệu thống kê đầy bất ngờ.

Tối Ưu Hóa Số Lượng Mặt Hàng Trong Đơn Hàng Lấy Hàng

Một câu hỏi tự nhiên nảy sinh là liệu tổng quãng đường di chuyển có luôn tăng khi số lượng mặt hàng cần lấy tăng lên hay không. Ban đầu, trực giác mách bảo rằng điều này là đúng. Tuy nhiên, điều thú vị là sau một ngưỡng nhất định, quãng đường này lại bắt đầu có xu hướng giảm dần! Điều này xảy ra bởi lẽ khi số lượng mặt hàng quá lớn, người vận hành cuối cùng sẽ phải dừng lại ở hầu hết các hành lang trong kho để lấy hàng. Tại thời điểm đó, khả năng sử dụng các "lối tắt" thông minh để rút ngắn tổng quãng đường dường như không còn hiệu quả nữa.

Một xu hướng rõ nét cho thấy rằng đối với hơn 15 đến 20 đơn vị trên mỗi lệnh lấy hàng, việc bổ sung thêm các mặt hàng dường như không làm tăng đáng kể tổng quãng đường di chuyển. Bởi lẽ, đến lúc này, bạn gần như phải đi qua tất cả các hành lang của kho để hoàn tất đơn hàng. Điều đáng lưu ý là những phân tích này thường được minh họa qua các biểu đồ mật độ, thể hiện sự phân bố quãng đường di chuyển điển hình cho mỗi lệnh lấy hàng.

Phân Tích Quãng Đường Di Chuyển Trên Từng Mặt Hàng

Một thống kê thú vị khác, hé lộ một xu hướng tương tự, là phân phối quãng đường di chuyển trên mỗi mặt hàng được chọn. Chúng ta có thể thấy rằng đối với các danh sách lấy hàng có ít mặt hàng, quãng đường di chuyển trung bình cho mỗi mặt hàng có xu hướng tương đối cao, và đặc biệt là có phương sai lớn. Điều này phụ thuộc nhiều vào yếu tố "may mắn" khi các mặt hàng tình cờ nằm gần nhau hoặc trong cùng một hành lang. Ngược lại, đối với các danh sách lấy hàng chứa nhiều mặt hàng, quãng đường di chuyển trên mỗi mặt hàng lại giảm dần một cách rõ rệt. Chính vì vậy, loại thống kê này cực kỳ hữu ích để nghiên cứu sâu hơn, nhằm tối ưu hóa số lượng mặt hàng nên có trong mỗi danh sách lệnh lấy hàng, với mục tiêu cuối cùng là giảm thiểu quãng đường di chuyển cho từng mặt hàng được chọn.

Tối Ưu Hóa Chi Phí Vận Chuyển Dựa Trên Dữ Liệu Khách Hàng

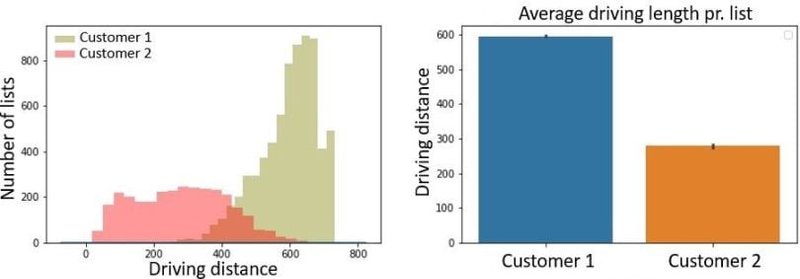
Tôi đã áp dụng dữ liệu thực tế, trong đó bao gồm cả thông tin bổ sung dưới dạng mã khách hàng, tập trung vào hai khách hàng cụ thể. Từ đó, chúng ta có thể đi sâu hơn vào phân tích sự phân bố quãng đường di chuyển trên mỗi danh sách đơn hàng lấy hàng của hai khách hàng này. Chẳng hạn, liệu có sự khác biệt đáng kể về quãng đường mà người vận hành phải đi để lấy hàng cho khách hàng này so với khách hàng kia không? Và nếu có, liệu chúng ta có nên cân nhắc tính thêm phí cho khách hàng yêu cầu quãng đường di chuyển dài hơn, nhằm bù đắp chi phí vận hành tăng thêm?

Khi xem xét phân phối quãng đường di chuyển của Khách hàng 1 và Khách hàng 2, một điểm đáng chú ý là đối với Khách hàng 2, phần lớn các danh sách lệnh lấy hàng đều có quãng đường lái xe ngắn hơn đáng kể so với Khách hàng 1. Sự khác biệt này càng trở nên rõ ràng hơn khi chúng ta so sánh số dặm trung bình cho mỗi danh sách lệnh lấy hàng của hai khách hàng. Khách hàng 2 thường xuyên yêu cầu quãng đường di chuyển ít hơn.

Loại thông tin quý giá này có thể được ứng dụng để xây dựng các mô hình định giá sản phẩm linh hoạt. Giá thành sản phẩm cho khách hàng có thể được tính toán không chỉ dựa trên giá trị sản phẩm mà còn dựa trên tổng số kilomet đã di chuyển cho mỗi đơn hàng. Đối với những khách hàng có đơn hàng đòi hỏi quãng đường di chuyển nhiều hơn, kéo theo thời gian và chi phí vận hành cao hơn, doanh nghiệp hoàn toàn có thể cân nhắc áp dụng mức phí bổ sung, tạo sự công bằng hơn so với các đơn hàng có quãng đường di chuyển ngắn.

Tại sao lý thuyết đồ thị lại quan trọng?

Lý thuyết đồ thị, tưởng chừng như một lĩnh vực toán học thuần túy và trừu tượng, thực chất lại ẩn chứa một kho tàng ứng dụng vô cùng phong phú và hấp dẫn trong thế giới thực. Chúng ta sẽ cùng khám phá tại sao ngành khoa học này lại trở nên thiết yếu đến vậy, không chỉ để giải quyết những bài toán hóc búa mà còn để thỏa mãn niềm đam mê khám phá những điều kỳ diệu ẩn sau các mối quan hệ phức tạp. Hy vọng rằng những kiến thức nền tảng và ví dụ dưới đây sẽ hữu ích cho việc tiếp cận các vấn đề tương tự sau này, hoặc ít nhất là khơi gợi thêm sự tò mò của bạn về thế giới đồ thị đầy mê hoặc.

Lý thuyết đồ thị là gì?

Lý thuyết đồ thị là một nhánh nghiên cứu toán học tập trung vào cấu trúc dữ liệu đồ thị, nơi chúng ta dùng các đỉnh (nút) để biểu diễn các đối tượng và các cạnh để minh họa mối quan hệ giữa chúng. Mầm mống của lý thuyết này đã nảy sinh từ thế kỷ 18, khi nhà toán học vĩ đại Leonhard Euler tìm lời giải cho bài toán nổi tiếng về Bảy cây cầu ở Königsberg. Ngày nay, lý thuyết đồ thị trở thành công cụ đắc lực để mô hình hóa, phân tích mạng lưới, tối ưu hóa các tuyến đường và gỡ rối những hệ thống phức tạp nhất trong thực tiễn.

Có những loại đồ thị chính nào?

Trong thế giới đồ thị, chúng ta thường gặp ba loại hình cơ bản, mỗi loại mang một đặc điểm và ứng dụng riêng biệt:

• Đồ thị vô hướng: Tại đây, các cạnh nối giữa các đỉnh không mang một chiều cố định; mọi "con đường" đều có thể đi được theo hai chiều, tựa như một con đường giao thông hai chiều vậy.
• Đồ thị có hướng (DiGraph): Khác với đồ thị vô hướng, mỗi cạnh trong đồ thị này đều sở hữu một hướng đi xác định, giống như những con đường một chiều chỉ cho phép di chuyển theo một hướng duy nhất.
• Đồ thị có trọng số: Đây là loại đồ thị mà mỗi cạnh không chỉ có hướng mà còn được gán thêm một "trọng số" cụ thể. Trọng số này thường dùng để biểu thị khoảng cách, chi phí, thời gian, hay bất kỳ đại lượng nào khác, rất hữu ích trong việc tìm ra đường đi ngắn nhất hoặc tối ưu nhất.

Những ứng dụng thực tế nổi bật của lý thuyết đồ thị là gì?

Từ lý thuyết, lý thuyết đồ thị đã bước ra đời thực và trở thành một phần không thể thiếu trong nhiều lĩnh vực: từ phân tích mạng xã hội, tối ưu hóa định vị GPS, cải thiện thuật toán xếp hạng công cụ tìm kiếm, đến việc quản lý hiệu quả hậu cần kho bãi, hỗ trợ giải trình tự DNA, và củng cố bảo mật mạng máy tính. Sức mạnh của nó nằm ở khả năng mô hình hóa và giải quyết những thách thức phức tạp nhất của thế giới hiện đại.