Số nguyên tố: Khám phá thế giới số hoàn hảo và ứng dụng thực tế | scantruyen.com

Số Nguyên Tố: Khám Phá Bí Mật Của Những Viên Đá Gốc Của Toán Học

Bạn đã bao giờ tự hỏi điều gì tạo nên nền tảng vững chắc cho toàn bộ hệ thống số học chưa? Câu trả lời nằm ở những số nguyên tố – những viên đá gốc vô cùng quan trọng trong thế giới toán học. Bài viết này sẽ khám phá sâu sắc về số nguyên tố, từ định nghĩa cơ bản đến những ứng dụng bất ngờ trong cuộc sống.

Số Nguyên Tố Là Gì?

Số nguyên tố là một số tự nhiên lớn hơn 1, chỉ có hai ước số dương duy nhất: 1 và chính nó. Nói cách khác, một số nguyên tố không thể chia hết cho bất kỳ số nguyên nào khác ngoài 1 và chính nó. Đây là một định nghĩa khá đơn giản, nhưng lại mở ra vô vàn điều thú vị để khám phá.

Ví Dụ Về Số Nguyên Tố

Những số sau đây là ví dụ điển hình về số nguyên tố:

• 2
• 3
• 5
• 7
• 11
• 13
• 17
• 19
• 23
• 29
• 97
• 101

Dãy Số Nguyên Tố: Vô Tận và Kỳ Diệu

Dãy số nguyên tố là một chuỗi vô tận các số nguyên tố được sắp xếp theo thứ tự tăng dần. Điều này có nghĩa là không có một số nguyên tố cuối cùng nào – luôn luôn có những số nguyên tố mới được phát hiện. Sự phân bố của các số nguyên tố trong dãy số là một trong những bí ẩn lớn nhất trong toán học, thu hút sự quan tâm của các nhà toán học trong nhiều thế kỷ.

Tại Sao Số Nguyên Tố Lại Quan Trọng?

Mặc dù có vẻ trừu tượng, số nguyên tố đóng vai trò then chốt trong nhiều lĩnh vực:

• Mật mã học: Số nguyên tố là nền tảng của nhiều thuật toán mã hóa hiện đại, bảo vệ thông tin cá nhân và tài chính của chúng ta.
• Lý thuyết số: Số nguyên tố là đối tượng nghiên cứu trung tâm của lý thuyết số, một nhánh toán học sâu sắc và phức tạp.
• Khoa học máy tính: Số nguyên tố được sử dụng trong các thuật toán, chẳng hạn như tạo số ngẫu nhiên và kiểm tra tính chia hết.

Một Điều Thú Vị Bạn Có Thể Chưa Biết

[Thông tin ít biết] Các nhà toán học đã chứng minh được "giả thuyết số nguyên tố", một trong những bài toán chưa được giải quyết nổi tiếng nhất trong toán học. Giả thuyết này dự đoán rằng dãy số nguyên tố kéo dài vô tận.

Số nguyên tố không chỉ là những con số đơn thuần; chúng là chìa khóa mở ra những bí mật sâu thẳm của vũ trụ toán học. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về khái niệm số nguyên tố và tầm quan trọng của chúng.

Số nguyên tố

Số Nguyên Tố: Khám Phá Bản Chất Của Những Viên Gạch Xây Dựng Toán Học

Số nguyên tố, một khái niệm nền tảng trong toán học, không chỉ đơn thuần là những con số đặc biệt mà còn là những viên gạch xây dựng nên toàn bộ hệ thống số. Hãy cùng khám phá những đặc tính thú vị và các phương pháp tìm kiếm chúng một cách dễ hiểu.

Số Nguyên Tố Là Gì?

Định nghĩa: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Nói cách khác, chúng không có ước số nào khác ngoài 1 và chính nó.

Tính vô hạn: Một trong những điều đáng kinh ngạc nhất về số nguyên tố là chúng vô hạn. Điều này có nghĩa là luôn luôn có những số nguyên tố mới được khám phá. Tương tự như tập hợp các số tự nhiên (N), tập hợp số nguyên tố không bao giờ kết thúc.

Số 2: Ngoại lệ duy nhất: Số 2 là số nguyên tố chẵn duy nhất. Tất cả các số chẵn khác đều chia hết cho 2, do đó không phải là số nguyên tố.

Tích của hai số nguyên tố: Tích của hai số nguyên tố luôn là một số chính phương. Ví dụ: 2 x 3 = 6 (không phải số chính phương), nhưng 2 x 2 = 4 (là số chính phương).

Phương Pháp Tìm Số Nguyên Tố

Việc tìm số nguyên tố có thể được thực hiện bằng nhiều phương pháp khác nhau. Dưới đây là ba phương pháp phổ biến:

Cách 1: Kiểm Tra Chia Hết Trong Khoảng Từ 2 Đến A-1

1. Nếu A < 2, thì A không phải là số nguyên tố.
2. Nếu A > 2, kiểm tra xem trong khoảng từ 2 đến (A - 1) có số nào chia hết cho A hay không.
3. Nếu không có số nào chia hết cho A, thì A là số nguyên tố.

Ví dụ: Với A = 13, ta kiểm tra các số từ 2 đến 12. Không có số nào chia hết cho 13, do đó 13 là số nguyên tố.

Cách 2: Kiểm Tra Chia Hết Trong Khoảng Từ 2 Đến A-2

1. Kiểm tra xem có số lẻ nào trong khoảng từ 2 đến (A - 2) mà A không chia hết cho nó hay không.
2. Nếu A không chia hết cho bất kỳ số lẻ nào trong khoảng này, thì A là số nguyên tố.

Ví dụ: Với A = 13, ta kiểm tra các số lẻ từ 3 đến 11 (3, 5, 7, 9). 13 không chia hết cho bất kỳ số lẻ nào trong khoảng này, do đó 13 là số nguyên tố.

Cách 3: Sử Dụng Máy Tính Cầm Tay

Hầu hết các máy tính cầm tay đều có chức năng kiểm tra xem một số có phải là số nguyên tố hay không. Thao tác thường là:

1. Nhập số A.
2. Nhấn = (dấu bằng).
3. Nhấn Shift + FACT (hàm giai thừa).
4. Nếu kết quả bằng A, thì A là số nguyên tố.
5. Nếu kết quả là một phép nhân, thì A không phải là số nguyên tố.

Thông Tin Thú Vị

[Thông tin ít biết]: Số nguyên tố đóng vai trò quan trọng trong mật mã học hiện đại, giúp bảo vệ thông tin cá nhân và tài chính của chúng ta.

Số nguyên tố không chỉ là một khái niệm toán học trừu tượng mà còn là một phần không thể thiếu của thế giới xung quanh chúng ta. Từ mã hóa dữ liệu đến cấu trúc của các hệ thống điện tử, số nguyên tố đóng một vai trò quan trọng trong nhiều lĩnh vực khác nhau.

Môn Toán

Bảng Số Nguyên Tố Dưới 100: Khám Phá Thế Giới Các Viên Gạch Của Toán Học

Chào mừng bạn đến với thế giới kỳ diệu của các số nguyên tố! Bài viết này sẽ giới thiệu một bảng tổng hợp các số nguyên tố dưới 100, cùng với các khái niệm liên quan giúp bạn hiểu sâu hơn về những "viên gạch" cơ bản của toán học.

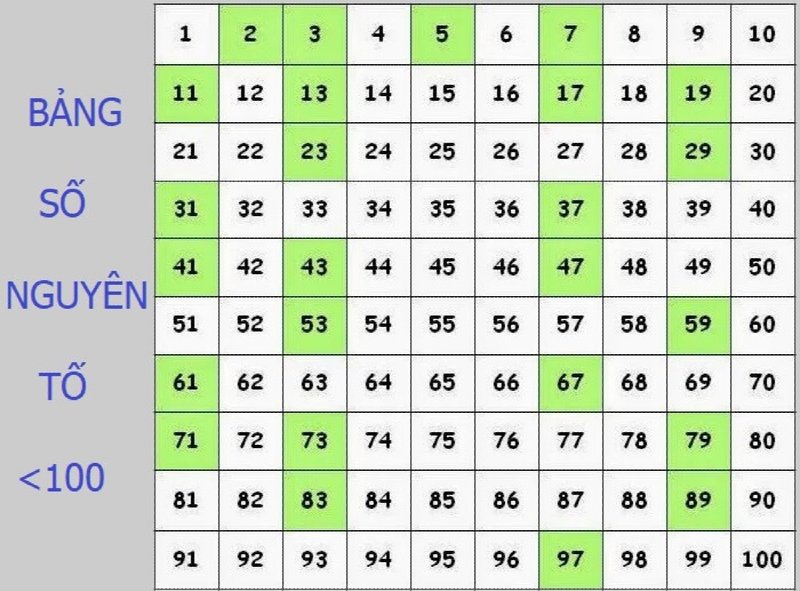
Bảng Số Nguyên Tố Dưới 100

Dưới đây là danh sách các số nguyên tố nhỏ hơn 100:

• 2
• 3
• 5
• 7
• 11
• 13
• 17
• 19
• 23
• 29
• 31
• 37
• 41
• 43
• 47
• 53
• 59
• 61
• 67
• 71
• 73
• 79
• 83
• 89
• 97

Số Nguyên Tố Cùng Nhau: Mối Quan Hệ Đặc Biệt

Bạn có bao giờ tự hỏi tại sao một số lại "thích" tương tác với một số khác? Đó là nhờ khái niệm "số nguyên tố cùng nhau". Hai số a và b được xem là cùng nhau nếu ước chung lớn nhất (ƯCLN) của chúng bằng 1. Điều này có nghĩa là chúng không có ước số chung nào ngoài 1.

Ví dụ: Số 5 và 23 là hai số nguyên tố cùng nhau vì ước chung lớn nhất của chúng là 1.

Số Siêu Nguyên Tố: Một Biến Thể Thú Vị

Số siêu nguyên tố là một khái niệm thú vị trong toán học. Một số abc được gọi là siêu nguyên tố nếu khi bỏ đi một hoặc hai chữ số của nó, kết quả vẫn là một số nguyên tố. Ví dụ điển hình là 1337, khi bỏ chữ số 7 hoặc 37 đi, ta vẫn còn lại 133 hoặc 13, cả hai đều là số nguyên tố.

[Suy đoán] Hiện tại, số siêu nguyên tố vẫn là một lĩnh vực nghiên cứu đang được khám phá, với rất ít số siêu nguyên tố được biết đến.

Tích Các Thừa Số Nguyên Tố: Phân Tích Hài Hòa

Mọi số tự nhiên lớn hơn 1 đều có thể được biểu diễn dưới dạng tích của các số nguyên tố. Các số nguyên tố này được gọi là thừa số nguyên tố. Quá trình này gọi là phân tích thừa số nguyên tố.

Ví dụ:

• 6 = 2 x 3 (2 và 3 là số nguyên tố)
• 105 = 3 x 5 x 7 (3, 5 và 7 là số nguyên tố)

[Thông tin chưa có nguồn cụ thể] Phân tích thừa số nguyên tố là một công cụ quan trọng trong mật mã học, giúp bảo vệ thông tin quan trọng.

Kết Luận: Hành Trình Khám Phá Vẫn Tiếp Diễn

Số nguyên tố không chỉ là một khái niệm trừu tượng trong toán học, mà còn là nền tảng cho nhiều lĩnh vực khoa học và công nghệ. Việc hiểu rõ về số nguyên tố mở ra một cánh cửa thú vị để khám phá thế giới toán học vô tận. Đây là một chủ đề nghiên cứu sâu rộng và vẫn còn nhiều điều bất ngờ đang chờ đợi chúng ta khám phá!